一类带交叉扩散项的捕食-食饵模型全局分歧研究
宋倩倩,李艳玲
陕西师范大学 数学与信息科学学院,西安 710119
近年来,随着种群生态学的发展,捕食系统已经成为数学和生物学领域的一个重要课题,据此研究者已经建立了包括Lotka-Volterra模型、比率型、Holling-Leslie模型等在内的多种捕食食饵模型.文献[1]给出如下带有扩散项的Holling-Leslie捕食食饵模型
(1)
文献[1]主要研究该系统周期轨道的存在性和非常数正解的全局稳定性.文献[2]主要研究系统(1)中b=1的情况下正解存在性与其分歧解的局部和全局稳定性.
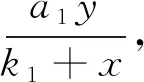
其次,种群间的相互影响在种群扩散中起着非常重要的作用[6-12].其中:文献[6]解释了一类具有交叉扩散项的生物意义并讨论捕食食饵模型非常数正解存在性:文献[7-8] 研究了一类带交叉扩散项的的局部分歧正解情况:文献[9]研究了空间不均匀环境下带交叉扩散项的Lotka-Volterra竞争模型正解问题.然而目前在齐次Dirichlet边界条件下研究带有交叉扩散项和优化的Leslie-Gower型反应函数系统的研究工作所见不多.故本文受文献[4,7-8]的启发在文献[1]的基础上研究如下带有修正的Leslie-Gower模型和交叉扩散项的竞争模型
(2)
其中:Δ为Lapalce算子:Ω为Rn中具有光滑边界的有界开区域:u,v分别表示食饵和捕食者的种群密度:α,β,a,b,m,k都是正常数,α和β代表交叉扩散系数,a和b分别表示食饵种群和捕食者种群的内禀增长率,齐次的Dirichlet边界条件意味着两个物种的居住区域Ω被一个敌对的环境所包围.
在食物严重缺乏的情况下区别于模型(1)的反应函数,模型(2)中优化的Leslie-Gower型反应函数表明,即使食饵数量急剧减少也不会对捕食者数量的增长产生较大的影响.此外,模型(2)中还增加了二者之间的交叉扩散项,这使模型更具有实际的生物意义.
1 正解的先验估计
-μΔψ+q(x)ψ=λψ,x∈Ω:ψ=0,x∈∂Ω
λ1(q(x))关于q(x)递增.记λ1(0)=λ1,对应的主特征函数记作ψ1(ψ1>0,x∈Ω).
考虑非线性边值问题
-Δu=u(a-u),x∈Ω:u=0,x∈∂Ω
(3)
若a<λ1,则u=0是(3)式的唯一非负解:若a>λ1,则(3)式有唯一正解,记为θa,θa关于a单调递增.
同理,考虑非线性边值问题
-Δv=v(b-βv),x∈Ω:v=0,x∈∂Ω
(4)
若b<λ1,则v=0是(4)式的唯一非负解:若b>λ1,则(4)式有唯一正解,记为θb,θb关于b单调递增.以上结论可参考文献[13].
令
U=(1+αv)uV=(1+βu)v
由于

(5)

引理1若a≤λ1或者b≤λ1,则方程(5)没有正解.
证假设方程(5)有正解(U,V),由方程(5)关于U的方程可得
两边同乘U,在Ω上积分,结合Green公式得
引理2若a,b>λ1,(U,V)是方程(5)的任一正解,则对于任意的x∈Ω,有
0 由于 从而有 进而有v(x0) U(x)≤U(x0)=(1+αv(x0))u(x0)<(1+αau(x0))u(x0)≤a(1+αa2) 同理可得 v(x1) V(x)≤V(x1)=(1+βu(x1))v(x1)≤(1+βM(a))·b(k+a) 从而定理得证. 由于分歧正解的存在性与特征值问题密切相关,因此在讨论分歧正解的存在性之前给出两个与分歧正解存在性相关的特征值引理. 令 其中(u,v)是(U,V)的函数,将(3)式在(U,V)=(θa,0)处Taylor展开得 (6) 其中(6)式中偏导数均为(θa,0)处的导数值,Qi(a:U-θa,V)满足Qi(a:U-θa,V)(0,0)=0,i=1,2,且有 定理1设a>λ1,b>λ1,则(a*:θa,0)∈R+×X为系统(5)的分歧点,且在(a*:θa*,0)的邻域内存在正解,即 Γ*={(a(s):θa*+s(φ*+φ1(s)),s(ψ*+ψ1(s))):0 (7) (8) 因此算子L(a*:0,0)的核空间N(L(a*:0,0))=span{(φ*,ψ*)T}.令L*(a*:0,0)为L(a*:0,0)的自伴算子,经计算L*(a*:0,0)(φ,ψ)=0等价于 (9) 因此得 dimN(L(a*:0,0))=1 codimR(L(a*:0,0))=1 (10) 那么有 两边同时乘ψ*,然后在Ω上积分,结合Green公式得 由于 所以有 (11) 由于θa关于a严格单调递增,则(11)式左边大于0.从而矛盾,即L1(a*:0,0)(φ*,ψ*)∉R(L(a*:0,0)). 同理可得发自半平凡解分支(a*:0,kθb)的局部分歧正解. 定理2设a,b>λ1,则(a*:0,kθb)∈R+×X为系统(5)的分歧点,且在(a*:0,kθb)的邻域内存在正解,即 Γ*={(a(s):s(φ*+φ2(s)),θb+s(ψ*+ψ2(s))):0 定理3若a,b>λ1,则由定理1给出的分歧正解Γ*在正锥P内可延拓为全局分歧,并且存在常数a∞充分大,使得当a>a∞时,全局分歧曲线随参数a延伸到无穷. 证(7)式等价于 (12) (13) (14) 若η≡0,由算子(-μΔ-a+2θa)可逆知ξ≡0,矛盾,则η≠0.令 令a>a*,∀μ≥1,i≥0有λi(μ,ha*)≥λ2(μ,ha*)>λ1(1,ha*).因此,K′(a)没有大于或等于1的特征值.此时有i(K(a:·),0)=1. (15) 其中 下面证μ1的代数重数为1.只需证 R(μ1I-K′(a))∩N(μ1I-K′(a))=0 即 (16) (17) 另外,结合(16)式可得 与ha<0矛盾.故μ1的代数重数为1.因此当a*-γ C1=C0-{(a(s):s(φ*+φ1(s)),s(ψ*+ψ1(s))):-σ 则C为系统(5)由(a*:θa*,0)的解曲线,在(a*:θa*,0)的小邻域内有C∈P,而且分支C-{(a*:θa*,0)}满足下列条件之一: 2)C在R+×P内由(a*:θa*,0)延伸到∞. 下面证明C-{(a*:θa*,0)}⊆P.假设C-{(a*:θa*,0)}P,则存在点和序列{an,Un,Vn}⊆C∩P,Un>0,Vn>0,使得n→∞时,(an,Un,由于(un,vn)和(Un,Vn)之间存在一一对应的关系知(un,vn)(θa,0).因此或 通过以上讨论知3)成立,即C-{(a*:θa*,0)}⊆P.因为‖Un‖∞,‖Vn‖∞有界.则全局分歧曲线只能沿参数a延伸到∞. 注2注意到(u,v)≥(0,0)和(U,V)≥(0,0)之间存在一一对应的关系,由定理1和定理2知模型(5)存在分歧正解. 本节参考文献[14]的方法主要分析了系统(5)的平凡解和半平凡解的稳定性.显然系统(5)的平凡解是(0,0),半平凡解是(θa,0)(a>λ1),(0,kθb)(b>λ1). 定理41) 若a<λ1且b<λ1,则平凡解(0,0)是渐近稳定的:相反地,若a>λ1或者b>λ1,则平凡解(0,0)是不稳定的. 证因为3种情况的证明过程相似,所以在此只证定理4中的情况(2).由线性化原理知,(θa,0)的稳定性由下面特征值问题决定 (18) 由于(18)中的方程不是完全对称的,需要考虑下面两个特征值问题 (19) 和 (20) 由文献[14]知(18)式的特征值是(19)式和(20)式的组合.分别记(19)式和(20)式的特征值为λ*和λ*,则有 λ*=λ1(2θa-a)>λ1(θa-a)=0 为了研究λ*,因V=(1+βu)v,则由主特征值的变分原理得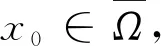
2 分歧正解的存在性








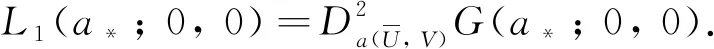


3 局部分歧解的延拓













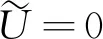

4 平凡解和半平凡解的稳定性





