一道向量组线性相关性试题的多种解法及其思政元素

朱凤娟

(北方民族大学 数学与信息科学学院,宁夏 银川 750021)

习近平总书记强调：“做好高校思想政治工作,要因事而化、因时而进、因势而新.要遵循思想政治工作规律,遵循教书育人规律,遵循学生成长规律,不断提高工作能力和水平.要用好课堂教学这个主渠道,思想政治理论课要坚持在改进中加强,提升思想政治教育亲和力和针对性,满足学生成长发展需求和期待,其他各门课都要守好一段渠、种好责任田,使各类课程与思想政治理论课同向同行,形成协同效应”[1].习近平总书记的重要论述是课程思政建设的科学指南,赋予课程思政建设理论认知、方法认知和精髓要义,指明了课程思政建设前进的方向．2020年5月,教育部出台了《高等学校课程思政建设指导纲要》，以下简称《纲要》.《纲要》明确指出：“落实立德树人根本任务,必须将价值塑造、知识传授和能力培养三者融为一体、不可割裂.全面推进课程思政建设,就是要寓价值观引导于知识传授和能力培养之中,帮助学生塑造正确的世界观、人生观、价值观,这是人才培养的应有之义,更是必备内容”[2].《纲要》明确了课程思政建设的目标要求、重点内容、建设路径和教师作用等等.在立德树人的工作中,价值比能力和知识更加重要；价值塑造是育人工作的第一要务,要将价值塑造的成分有机地融入能力培养和知识传授之中；要充分发掘各类课程所蕴含的思政要素,做到春风化雨、沁人心田,切实达到育人成效[3].专业课与“思政教育”同向同行,发挥好专业课程的育人功能,能更为“隐性”而有效地达成思想政治教育的成效,培养德智体美劳全面发展的社会主义建设者和接班人[4].

1 线性代数课程思政的重要意义

线性代数是理工经管类专业的一门数学基础课程.该课程主要讲授行列式、矩阵、线性方程组、二次型、线性变换与线性空间等线性代数的基本概念、基本理论和基本方法,通过课程的系统学习,旨在提高学生的逻辑思维和抽象思维能力,培养学生分析问题与解决问题的能力,并为后续课程打下必备的数学基础.因此,如何挖掘线性代数课程中的思想政治教育元素与德育元素并将它们润物细无声地融入到在课堂教学过程中是实施线性代数课程思政的核心与关键问题,从而实现知识传授、能力培养和价值引领的有机统一.文献[5-7]探讨了线性代数课程思政的教学设计与教学实践.

2 线性代数课程思政教学案例的设计

向量组线性相关性是研究线性方程组、线性空间和线性变换的基础,是线性代数的重点内容也是难点内容之一.下面,以向量组线性相关性的一道试题的多种证明方法为例,在引导学生更好地理解线性相关与线性无关的定义、学会运用线性相关与线性无关的性质和熟练掌握线性相关性的判定方法的同时,挖掘其蕴含的课程思政元素和德育元素,从而实现知识传授、能力培养和价值引领的有机统一的目标.

例设m维向量组α1,α2,α3线性无关,证明，向量组α1+α2,α2+2α3,α3+3α1也线性无关.

为了证明方便,先给出本文所需要的几个性质.

性质1[8-9]m维向量组α1,α2,…,αn(n≥2)线性无关的充要条件是向量组中任意一个向量都不能由其余n-1个向量线性表出.

性质2[8-10]m维向量组α1,α2,…,αn(n≥2)线性相关的充要条件是向量组中存在某一个向量可以由其余n-1个向量线性表出.

性质3[8-10]向量组线性无关(相关)的充要条件是向量组的秩等于(小于)向量组所含向量的个数.

直接利用向量组线性无关的定义证明.该方法是大多数线性代数教材所使用的方法,也是最直接和最简单的传统方法.

方法1设存在数k1,k2,k3使得

k1(α1+α2)+k2(α2+2α3)+k3(α3+3α1)=0,

(1)

则有

(k1+3k3)α1+(k1+k2)α2+(2k2+k3)α3=0.

(2)

由于向量组α1,α2,α3线性无关,故

(3)

k1=k2=k3=0.因此,向量组α1+α2,α2+2α3,α3+3α1线性无关.

利用向量组线性无关的性质证明,即利用性质1进行证明.该证明方法属于传统方法之一.在准确把握数学概念和定义基础上,进一步理解概念性质(内涵和外延),有利于培养学生求真的科学精神.

方法2证明向量组α1+α2,α2+2α3,α3+3α1中任意一个向量都不能由其他两个向量线性表出,总共有三种情况.首先，证α1+α2不能由α2+2α3,α3+3α1线性表出.假设存在数k1,k2使得

α1+α2=k1(α2+2α3)+k2(α3+3α1),

(4)

成立.则有

(1-3k2)α1+(1-k1)α2-(2k1+k2)α3=0.

由于向量组α1,α2,α3线性无关,故

(5)

显然线性方程组(5)无解,这说明不存在数k1,k2使得(4)式成立,即α1+α2不能由α2+2α3,α3+3α1线性表出.

同理可以证明向量α2+2α3不能由α1+α2,α3+3α1线性表出,以及向量α3+3α1不能由α1+α2,α2+2α3线性表出.

综上所述,向量组α1+α2,α2+2α3,α3+3α1线性无关.

应用向量组线性相关的定义采用反证法进行证明,该证明方法属于传统方法之一.线性相关和线性无关是两个相互对立的数学概念,非此即彼.

方法3假设向量组α1+α2,α2+2α3,α3+3α1线性相关,则一定存在一组不全为零的数k1,k2,k3使得

k1(α1+α2)+k2(α2+2α3)+k3(α3+3α1)=0,

则有

(k1+3k2)α1+(k1+k2)α2+(2k2+k3)α3=0.

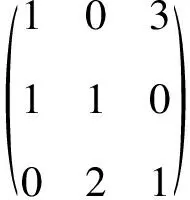
通过方法1至方法3的讲解,可以挖掘的课程思政元素为：鼓励学生追本溯源并使学生能把握问题的本质，在准确把握数学概念基础上,理解概念的内涵和外延.由浅入深地剖析命题.这样可以培养学生求真的科学精神,并启迪学生求知欲望,激发学生创新潜能.

利用向量组线性相关的性质进行反证,即利用性质2进行证明,该证明方法不属于传统方法.在课堂讲授过程中,此方法有利于培养学生的抽象思维能力和逻辑思维能力.

方法4反证法.假设向量组α1+α2,α2+2α3,α3+3α1线性相关,则向量组α1+α2,α2+2α3,α3+3α1中一定存在某一个向量可以由其他两个向量线性表出.不妨设α1+α2可以由α2+2α3,α3+3α1线性表出.即存在数k1,k2使得

α1+α2=k1(α2+2α3)+k2(α3+3α1),

则有

(1-3k2)α1+(1-k1)α2-(2k1+k2)α3=0.

(6)

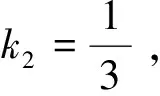
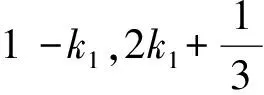
需要注意的是,在教学过程中对向量组线性相关要始终强调其存在性,向量组线性无关要始终强调其任意性.

将向量组的线性相关性与向量组的秩联系到一起,利用性质3进行证明.对于学生来讲,该证明方法已经将原问题进行了转化和延伸,有利于培养学生综合分析问题的能力.该方法已不属于传统方法.

方法5显然向量组α1+α2,α2+2α3,α3+3α1可以由向量组α1,α2,α3线性表出.根据矩阵乘法,有

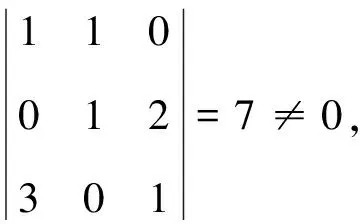
通过方法4到方法5讲解,可以挖掘到下面思政元素和德育元素: 鼓励学生要大胆探索,敢于追求真理,善于跳出固定思维,同时做到大胆假设、小心求证.告诉学生,解决问题的方法可能有多种,不要局限于书本上所讲的方法,更不能拘泥于传统方法.培养学生抽象思维能力和逻辑思维能力,特别是培养学生用抽象眼光看待世界的方法和为追求真理和理想而不断探索、吃苦耐劳的拼搏精神.

将向量组的线性无关性与向量组的秩、矩阵的秩以及矩阵的初等变换结合起来.利用矩阵的秩等于其行(列)向量组的秩以及矩阵初等变换不改变矩阵的秩等性质进行证明.对于学生来讲,该方法已经将原问题做了进一步转化和拓展,不仅有利于培养学生综合分析问题能力,有利于学生掌握以简驭繁、化繁为简等解决问题的方式,也有助于培养学生解决复杂问题的能力.该方法已不属于传统方法.

方法6把向量组α1,α2,α3看成矩阵A的列向量组,向量组α1+α2,α2+2α3,α3+3α1看成矩阵B的列向量组.对矩阵A做一系列的初等列变换

(7)

由(7)式知矩阵A经过一系列初等列变换可得到矩阵B,利用矩阵初等变换不改变矩阵秩的性质,得矩阵A的秩等于矩阵B的秩.又因为矩阵的秩等于其列向量组的秩,因此向量组α1,α2,α3的秩等于向量组α1+α2,α2+2α3,α3+3α1的秩.由性质3知向量组α1+α2,α2+2α3,α3+3α1线性无关.

方法7把向量组α1,α2,α3看成矩阵A的行向量组,向量组α1+α2,α2+2α3,α3+3α1看成矩阵B的行向量组.对矩阵A做一系列的初等行变换

(8)

由(8)式知矩阵A经过一系列初等行变换可得到矩阵B,利用矩阵初等变换不改变矩阵的秩的性质,得矩阵A的秩等于矩阵B的秩.又因为矩阵的秩等于其行向量组的秩,因此，向量组α1,α2,α3的秩等于向量组α1+α2,α2+2α3,α3+3α1的秩.由性质3知向量组α1+α2,α2+2α3,α3+3α1线性无关.

上述7种证明方法,证明过程从易到难,所运用知识点由少变多，综合性也逐渐增强,有助于训练学生的逻辑思维能力、综合分析与解决数学问题的能力.从中可以提炼到思政元素为:现实世界是多姿多彩的,也是纷繁复杂的,在学习、生活和工作中会面临各种各样机遇、困难和挑战,掌握从易到难、以简驭繁、化繁为简、善于转化等解决问题的方式,从而培养学生综合分析问题能力和解决复杂问题能力.

3 结语

专业课教师是思政育人之魂的关键核心,发挥着课程思政的主导作用.教师要在课程思政的教学设计上下功夫,要在课堂教学和教学策略上下功夫,让价值引导的成分融入课程设计和课堂教学,达到课程思政春风化雨和润物无声的育人效果.