基于伸缩因子的toric-Bézier曲线自由变形

王 涵，朱春钢

基于伸缩因子的toric-Bézier曲线自由变形

王 涵1，朱春钢2

(1. 山东工商学院计算机科学与技术学院，山东 烟台 264005； 2. 大连理工大学数学科学学院，辽宁 大连 116024)

为了得到理想的几何变形效果，将伸缩因子和toric退化理论作用到toric-Bézier曲线上，最终实现曲线的自由变形。首先给定提升函数构造出带参数的权因子集，从而得到带参数的toric-Bézier曲线；然后选取变形中心、变形区间以及变形区间边界光滑度，根据控制函数()的选取原则选取适当的控制函数，确定伸缩因子进而构造出变形矩阵，再将其作用到上述带参数的toric-Bézier曲线上；最后，当趋于无穷大时，得到目标曲线，实现toric-Bézier曲线的自由变形，通过交互改变控制参数，可达到预期的变形效果，并可给出toric-Bézier曲线的变形动画演示。实验表明，该技术计算简单、易于控制，可兼顾整体与局部对曲线进行自由变形，具有可调性和预见性，叠加使用可得到丰富的变形动画效果，适用于几何造型和计算机动画等领域。

几何造型；toric-Bézier曲线；提升函数；伸缩因子；自由变形

在几何造型和计算机动画领域，几何变形方法一直是一个热点研究课题。而自由变形技术是几何变形方法的典型代表。2010年，徐岗等[1]详细阐述了自由变形技术的发展与应用。1984年，BARR[2]提出整体与局部的变形方法，该方法及其推广能够进行如弯曲、扭曲、尖角等常规变形，但很难产生任意形状。为克服此难题，SEDERBERG和PARRY[3]在1986年提出了基于Bézier体的变形方法，首次提出了自由变形(free- form deformation，FFD)的概念，此方法被广泛应用于几何造型、计算机动画、科学数据可视化领域。1994年，CHANG和ROCKWOOD[4]提出了基于Bézier曲线de Casteljau算法的自由变形方法。BECHMANN和ELKOUHEN[5]则详细给出了该算法的实现过程。同年，LAZARUS等[6]提出了基于轴曲线的轴自由变形方法(axial deformations，AXDF)。1996年，FENG等[7]提出了基于参数曲面的自由变形方法。上述方法不同程度的改进了FFD的方法，使得在产生物体的变形方面具有良好的交互性和可控性。

在实际中，曲线变形也为人们所重视。所谓曲线变形就是曲线所在空间自身到自身的一个映射。近些年来，王小平等[8]提出了基于伸缩因子的曲线自由变形方法，基本思想是通过伸缩因子构造变形矩阵，然后将变形矩阵作用于一般参数曲线方程，从而实现曲线变形的目的。自此，陆续有多名学者发展此思想，通过改进伸缩因子来实现对参数曲线的变形。宋来忠等[9]通过对指数函数积分构造伸缩因子；刘植等[10]提出带参数的多项式伸缩因子；陆友太等[11]提出基于乘幂函数的伸缩因子；张莉等[12]提出基于平台函数的伸缩因子。以上伸缩因子实际应用起来各有利弊，但共同的优点是数学背景简单，易于操作和控制。因此，通过伸缩因子实现曲线的自由变形是可行的。

2002年，KRASAUSKAS[13]定义了一种多边形曲面——toric曲面(定义1)，该曲面与一个有限整数格点集相关。而且一维toric曲面经过一个简单的参数化可转换成经典的有理Bézier曲线，本文称之为toric-Bézier曲线(定义2)。在几何造型中，toric-Bézier曲线的控制结构具有良好的定义和几何意义。事实上，toric-Bézier曲线的形状不仅由控制顶点所定义的控制多边形所控制，而且还被其权因子所控制，当所有的权因子都足够大时，曲线被拉至相应的控制结构，即曲线的极限形式为正则控制曲线，该过程称为toric-Bézier曲线的toric退化[14]。Toric退化在曲线曲面的单值性[15]和等几何分析[16]中都有重要的应用。

本文将toric退化与伸缩因子相继作用到待变形toric-Bézier曲线上，最终实现曲线变形的目的。该技术基本思想如下：首先给定提升函数构造带参数的权因子集，从而得到带参数的toric- Bézier曲线；然后选定曲线变形中心、变形区间以及变形区间边界光滑度，根据控制函数的选取原则以及伸缩因子各参数的调控方式，选取连续控制函数()确定伸缩因子，进而构造出变形矩阵；最后将变形矩阵作用到上述带参数的toric- Bézier曲线上，受toric退化和伸缩因子的影响，当趋于无穷大时，实现toric-Bézier曲线的自由变形，同时可给出变形动画演示。最终实验表明，该技术计算简单、易于控制，可兼顾整体与局部对曲线进行自由变形，具有可调性和预见性，叠加使用可得到丰富的变形动画效果，适用于几何造型和计算机动画等领域。

1 Toric-Bézier曲线

1.1 Toric-Bézier曲线的定义

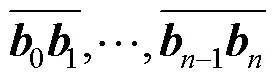
1.2 Toric-Bézier曲线的退化

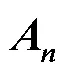
定理1[14].。

图1 三次toric–Bézier曲线及其控制多边形

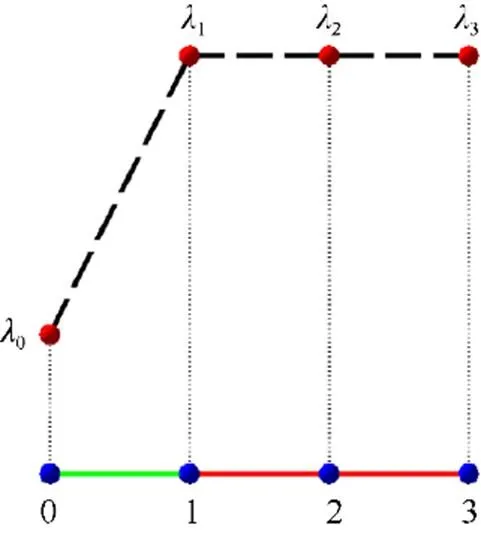
图2 提升函数λ诱导的正则分解

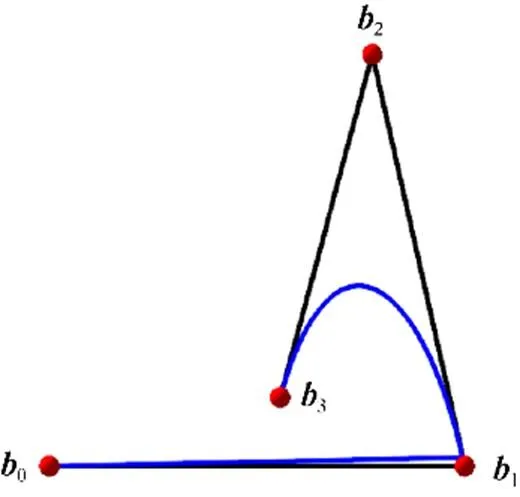
图3 正则控制曲线

例1中图1本为一条自交曲线，但是通过对其进行toric退化，使得最终得到的正则控制曲线避免了出现自交点的情况(图3)，保证了曲线的单值性，该性质在图像压缩、变形、三维变形和体变形中都有重要的作用。且利用toric退化对曲线做整体变形处理具有预见性，即当给定提升函数之后就可以分析出由其诱导的正则分解，从而预见变形后的曲线形状(即正则控制曲线)。

2 伸缩因子、曲线变形与控制

文献[8]提出的基于伸缩因子的曲线自由变形方法，不需要借助如FFD方法中的平行六面体格子或AXDF方法中的轴等辅助工具。不需要像Barr的方法先微分再积分，而是利用伸缩因子作用于待变形曲线方程，改变曲线形状。而且伸缩函数具有操作简单易行、可多参数调控以及支持局部变形等优点。本节对待变形toric–Bézier曲线同时作用toric退化和伸缩因子，可从整体与局部对曲线做自由变形处理，使得最终变形后的曲线形状具有可调性和预见性。

定义5.分段函数

称为伸缩因子，[0,1]为变形区间，其中正整数,≥2，()为控制函数。

伸缩因子的性质：

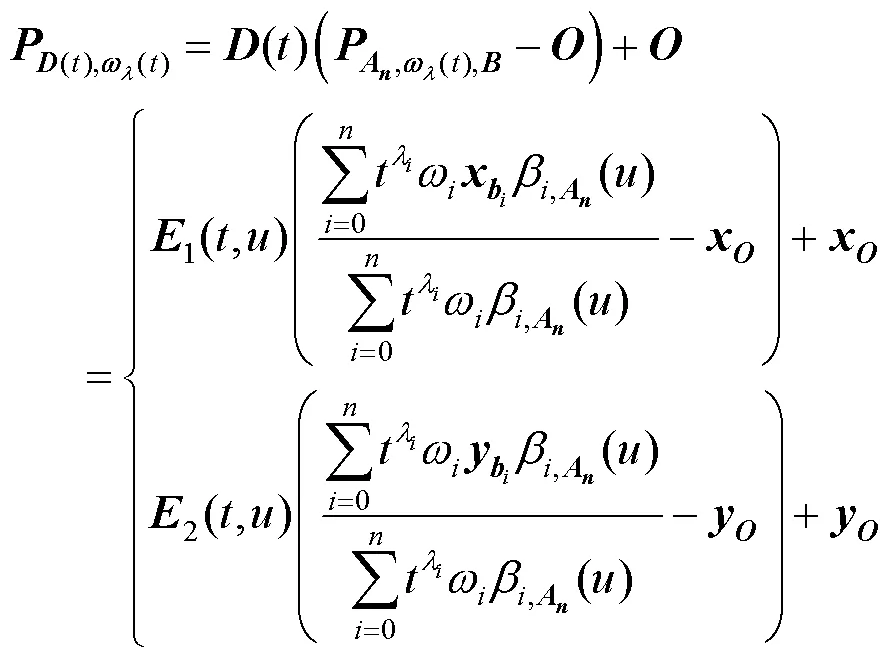
再根据定理1得

在实际应用中，通常一次自由变形不能得到理想的效果，需要对曲线进行多次自由变形，那么需要注意的是每次自由变形的变形区间是否为同一区间，因为相同的变形区间和不同的变形区间，叠加方法不同。

变形过程中，控制函数()的选取原则：

(1) 基于伸缩因子的曲线变形，不再受权因子和控制多边形的约束，曲线变形处的伸缩幅度会随着()值的增大而加大。因此，为了避免出现变形处伸缩幅度过大导致的极度变形效果，失去自由变形意义，特作如下约束，即

(2) 为了保证曲线能够在变形处实现动态变形，控制函数()应为连续函数，且值域范围应满足式(8)。而()的选取以形式简单为首要原则，如要加快变形速度，在满足式(8)的前提下，可适当选取次数较高的控制函数()。

变形过程中，伸缩因子和提升函数对toric– Bézier曲线变形的调控可通过以下方式实现：

(1) 控制函数()的正负值可以控制曲线变形处的伸缩方向，如图4中红色曲线部分所示(此时=10)，黑色点为曲线变形处的极值点，参数见表1，当参数≥0时，情形与情形，情形与情形的曲线变形处伸缩方向均关于垂直方向(即轴方向)对称，情形与情形，情形与情形的曲线变形处伸缩方向均关于水平方向(即轴方向)对称，情形与情形，情形与情形曲线变形处伸缩方向相反。

图4 f (t)的正负值可控制曲线的伸缩方向

表1 提升函数和伸缩因子参数表

(2)()值的大小可以控制曲线变形处的伸缩幅度，如图5中红色曲线部分所示(此时=10)，黑色点为曲线变形处的极值点，参数见表1，1()的值情形与情形相同，2()的值情形是情形的2倍，故情形变形处曲线的极值点高度是情形的2倍，同理情形与情形，情形与情形。

图5 f (t)值的大小可控制曲线的伸缩幅度

(3) 改变，可以使变形后曲线在变形区间边界光滑度发生变化，如图6中红色曲线部分所示(此时=10)，参数见表1，红色线在变形区间[1,2]端点处分别具有2阶光滑度，而红色虚线在其变形区间[1,2]端点处具有1阶光滑度。

图6 改变p，q可控制曲线在变形区间边界的光滑度

(4) 改变0，1可以控制曲线的变形区间，如图4～8中红色曲线部分所示，其中情形～的变形区间为[1,2]，情形的变形区间为[0,1]，情形的变形区间为[2,3]，参数见表1。

(5) 改变可以控制曲线的相对变形中心。如图4～8中红色曲线部分所示，其中情形～的变形中心为(1,1)，情形的变形区间为(3,1)，情形的变形区间为(2,1)，黑色点为曲线变形处的极值点，绿色点为曲线的相对变形中心，参数见表1。情形，，，，，，当1()与2()的取值范围均为正时，极值点远离变形中心；情形，当1()与2()的取值范围均为负时，极值点靠近变形中心；情形，当1()与2()的取值范围为一负一正时，极值点与情形的极值点关于轴方向对称，且轴方向靠近变形中心，轴方向远离变形中心；情形，当1()与2()的取值范围为一正一负时，极值点与情形的极值点关于轴方向对称，且轴方向远离变形中心，轴方向靠近变形中心。

图7 λ={1,3,1,3}，O=(3,1)

图8 λ={0,3,3,0}，O=(2,1)

实际应用时，可同时改变各控制参数，也可叠加使用得到丰富的变形动画效果。

从例2可以看出，伸缩因子的良好性质，可以对曲线做局部变形，且不受权因子和控制多边形的约束，从而实现自由变形。通过调控伸缩因子的各个参数以及提升函数，便可得到丰富的曲线变形效果。

3 实 例

本节共列举3个实例，给出toric–Bézier曲线的具体变形过程以及图示，其中图中红色表示在toric退化和伸缩因子双重作用下曲线的变形，蓝色则为仅在toric退化作用下曲线的变形。

图9 提升函数λ={1,1,1,1,1,1}曲线的变形动画演示((a)五次toric–Bézier曲线；(b) t=5；(c) t=10；(d) t=15)

表2 伸缩因子参数表

图10 不同的提升函数诱导出不同的变形效果

图9(d)是当提升函数取值={1,1,1,1,1,1}时的曲线变形动画效果，图10(a)为提升函数取值={1,3,3,3,2,1}时的曲线变形动画效果，图10(b)为提升函数取值={1,2,3,3,3,1}时的曲线变形动画效果。由于不同的提升函数诱导不同的正则控制曲线，即对曲线做不同的整体变形处理，所以不同的提升函数可以诱导出不同的曲线变形效果。

图11 Toric-Bézier曲线的变形动画演示

图12 提升函数λ={1,1,1}时得到的变形曲线

图13 提升函数λ={1,3,1}时得到的变形曲线

此例表明曲线的变形效果同样是受toric退化和伸缩因子的影响，兼顾整体与局部对待变形曲线做自由变形处理，得到的目标曲线多种多样，变形动画效果更加丰富。

4 总结与展望

本文主要通过对待变形toric-Bézier曲线同时作用toric退化和伸缩因子来实现对曲线的自由变形。与已有技术相比，具有以下优点：

(1) 此技术兼顾了整体和局部的自由变形处理。Toric退化可以对曲线做整体变形，伸缩因子可以自由选择变形区间对曲线做局部变形，并且在变形区间中不受权因子和控制多边形的约束，从而实现自由变形，同时也可以保证非变形区间不受影响。

(2) 利用toric退化对曲线做变形处理具有预见性，即当给定提升函数之后就可以分析出由其诱导的正则分解，从而预见目标曲线形状(即正则控制曲线)。

在以后的工作中，将继续研究toric-Bézier空间曲线和曲面的自由变形，希望得到更加丰富的曲线曲面变形动画效果。

[1] 徐岗, 汪国昭, 陈小雕. 自由变形技术及其应用[J]. 计算机研究与发展, 2010, 47(2): 344-352.

XU G, WANG G Z, CHEN X D. Free form deformation and its application[J]. Journal of Computer Research and Development, 2010, 47(2): 344-352 (in Chinese).

[2] BARR A H. Global and local deformations of solid primitives[J]. ACM SIGGRAPH Computer Graphics, 1984, 18(3): 21-30.

[3] SEDERBERG T W, PARRY S R. Free-form deformation of solid geometric models[J]. ACM SIGGRAPH Computer Graphics, 1986, 20(4): 151-160.

[4] CHANG Y K, ROCKWOOD A P. A generalized de Casteljau approach to 3D free-form deformation[C]//The 21st Annual Conference on Computer Graphics and Interactive Techniques - SIGGRAPH’94. New York: ACM Press, 1994, 28(4): 257-260.

[5] BECHMANN D, ELKOUHEN M. Animating with the “multidimensional deformation tool”[M]//Eurographics. Vienna: Springer Vienna, 2001: 29-35.

[6] LAZARUS F, COQUILLART S, JANCÈNE P. Axial deformations: an intuitive deformation technique[J]. Computer-Aided Design, 1994, 26(8): 607-613.

[7] FENG J Q, MA L Z, PENG Q S. A new free-form deformation through the control of parametric surfaces[J]. Computers & Graphics, 1996, 20(4): 531-539.

[8] 王小平, 叶正麟, 孟雅琴, 等. 基于伸缩因子的参数曲线自由变形[J]. 计算机辅助设计与图形学学报, 2002, 14(1): 66-69.

WANG X P, YE Z L, MENG Y Q, et al. Free-form deformation based on extension factor for parametric curve[J]. Journal of Computer Aided Design & Computer Graphics, 2002, 14(1): 66-69 (in Chinese).

[9] 宋来忠, 彭刚, 杨文颖, 等. 用于参数曲线自由变形的新的伸缩因子[J]. 工程图学学报, 2009, 30(3): 87-93.

SONG L Z, PENG G, YANG W Y, et al. A new extension factor for free-form deformation of parametric curves[J]. Journal of Engineering Graphics, 2009, 30(3): 87-93 (in Chinese).

[10] 刘植, 邬弘毅, 张莉, 等. 参数曲线曲面自由变形的多项式因子方法[J]. 计算机辅助设计与图形学学报, 2009, 21(3): 412-418.

LIU Z, WU H Y, ZHANG L, et al. Method of polynomial factor for free-form deformation of parametric curves and surfaces[J]. Journal of Computer-Aided Design & Computer Graphics, 2009, 21(3): 412-418 (in Chinese).

[11] 陆友太, 周来水, 王志国, 等. 基于乘幂伸缩因子的参数曲线自由变形[J]. 南京航空航天大学学报, 2011, 43(6): 793-798.

LU Y T, ZHOU L S, WANG Z G, et al. Free-form deformation based on power extension factor for parametric curves[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(6): 793-798 (in Chinese).

[12] 张莉, 余慧芳, 檀结庆. 带平台伸缩函数的参数曲线变形[J]. 中国图象图形学报, 2015, 20(10): 1374-1383.

ZHANG L, YU H F, TAN J Q. Deformation of parametric curves based on platform extension function[J]. Journal of Image and Graphics, 2015, 20(10): 1374-1383 (in Chinese).

[13] KRASAUSKAS R. Toric surface patches[J]. Advances in Computational Mathematics, 2002, 17(1): 89-113.

[14] GARC'IA-PUENTE L D, SOTTILE F, ZHU C G. Toric degenerations of Bézier patches[J]. ACM Transactions on Graphics, 2011, 30(5): 110.

[15] YU Y Y, JI Y, ZHU C G. An improved algorithm for checking the injectivity of 2D toric surface patches[J]. Computers & Mathematics With Applications, 2020, 79(10): 2973-2986.

[16] ZHU X F, JI Y, ZHU C G, et al. Isogeometric analysis for trimmed CAD surfaces using multi-sided toric surface patches[J]. Computer Aided Geometric Design, 2020, 79: 101847.

[17] 王涵. Toric曲面的正则控制曲面研究[D]. 大连: 大连理工大学, 2018.

WANG H. The regular control surfaces of toric patch[D]. Dalian: Dalian University of Technology, 2018 (in Chinese).

[18] WANG H, ZHU C G, ZHAO X Y. The number of regular control surfaces of toric patch[J]. Journal of Computational and Applied Mathematics, 2018, 329: 280-293.

Free-form deformation based on extension factor for toric-Bézier curve

WANG Han1, ZHU Chun-gang2

(1. School of Computer Science and Technology, Shandong Technology and Business University, Yantai Shandong 264005, China; 2. School of Mathematical Sciences, Dalian University of Technology, Dalian Liaoning 116024, China)

To gain ideal geometric deformation results, the expansion factor and the toric degeneration are applied to the toric-Bézier curve, realizing the free-form deformation of the curve. Firstly, the with parameterweight factor was constructed by the given lifting function, thereby obtaining thewith parametertoric-Bézier curve. Secondly, according to the selected center of deformation, region of deformation, smoothness of deformation region boundary, and select rule of the control function(), the appropriate control function was selected,and the extension factor was determined, thus constructing the deformation matrix. Then, the deformation matrix acted on the with parametertoric-Bézier curve. At last, whentended to reach infinity, the target curve was obtained, andthe free-form deformation of the toric-Bézier curve could be achieved. By changing the control parameters interactively, the expected deformation result could be attained, and the deformation animation demo of the toric-Bézier curve could be yielded. The experiments showed that the technique was simple and easy to control. The curve could be deformed freely both globally and locally, and the technique was of adjustability and foreseeability. Such a technique could be in repeated use, thereby generating the rich deformation animation results, which could be applicable to many fields, such as geometric modeling and computer animation.

geometric modeling;toric-Bézier curve; lifting function; extension factor; free-form deformation

TP 391

10.11996/JG.j.2095-302X.2022061070

A

2095-302X(2022)06-1070-10

2022-07-31；

：2022-10-24

国家自然科学基金项目(12001327，12071057)

王 涵(1988-)，女，讲师，博士。主要研究方向为计算几何、计算机图形学等。E-mail：wanghan19881214@126.com

朱春钢(1977-)，男，教授，博士。主要研究方向为计算几何、计算机辅助设计等。E-mail：cgzhu@dlut.edu.com

31 July，2022；

24 October，2022

National Natural Science Foundation of China (12001327, 12071057)

WANG Han (1988-), lecturer, Ph.D. Her main research interests cover computation geometry and computer graphics. E-mail：wanghan19881214@126.com

ZHU Chun-gang (1977-), professor, Ph.D. His main research interests cover computation geometry and computer aided design. E-mail：cgzhu@dlut.edu.com