带比例交易成本的Lévy风险模型中的最优分红和注资
候力佳,胡 华
(宁夏大学 数学统计学院,宁夏 银川 750021)
近年来,随着保险市场的高速发展,风险理论成为当今金融数学界和精算学界的重要研究内容之一,最优分红问题引起专家学者们的广泛关注,保险公司何时分红以及分红量的多少成为了学者们所要研究的一个重要问题.为了更好地刻画保险公司盈余过程并准确模拟金融市场运行规律Lévy过程满足这一特点且更符合实际,是非常重要的随机模型,具有如独立平稳增量性、马尔可夫性和无穷可分性等许多良好的性质,在随机分析等领域有着大量的研究和应用.
目前,关于保险公司分红与注资问题已有大量的研究成果[1-5],但是这些模型均假设分红可以在任何时候进行.然而,在现实生活中分红只能在一定的时间间隔内做出决定再进行分红.Albrecher等[6]在Cramér-Lundberg模型中首次提出了周期性障碍分红策略,其中破产和分红只能在某些随机观察时间才能被观察到.随后,具有周期性分红的风险模型得到了广泛的关注.Noba 等[7]讨论了谱负Lévy风险模型下的最优分红问题,其中分红是在独立泊松过程的跳跃时间下进行,证明了周期性障碍策略的最优性.Avanzi等[8]将固定交易成本纳入谱负Lévy过程,并对其最优周期分红问题进行了建模和研究,证明了在Lévy测度条件下周期分红策略是最优的.Avanzi等[9]考虑了一类具有持续支出和一次性收益的Lévy风险模型的分红问题,研究了固定交易成本对最优周期分红的影响策略,表明当决策时间根据在某个分红时刻,周期策略是一个最优的独立的泊松过程.Noba等[10]考虑了有救助条件下的谱负Lévy模型,证明了巴黎经典反射策略的最优性.钟玮[11]讨论了基于非指数折现函数的谱正Lévy模型下周期分红问题,给出了值函数满足的HJB方程并借助伊藤公式等得到了验证定理,结果表明在一定条件下周期障碍分红策略是均衡意义下的最优策略.
由于注资也是公司管理风险的常用手段,允许注资条件下的分红问题研究更加贴近现实,此时公司的价值可以重新定义为破产前分红现值与注资金值之差的期望值.注资是新的投资,应以换回足够的回报为前提,因此分红与注资同时优化就成了亟待解决的问题.而Lévy过程的样本路径具有间断点,可以刻画随机运动中的跳跃行为,带跳的Lévy过程具有非对称的尖峰厚尾性质和不连续性,克服了正态分布的对称性,可以很好地描述突发事件带来的影响,这使其更适用于刻画一些偶然的、极端的和特殊的随机波动模型,更符合实际情况的变化.Dong等[12]研究了具有两种分红的谱负Lévy风险模型在独立泊松观测时间下进行注资,通过尺度函数表示所有结果.Dong等[13]考虑了具有随机观测时间的谱负Lévy风险模型,分红和注资都是在独立泊松过程的观测时间下进行,在绝对破产情况下,讨论了预期贴现股息和预期的贴现注资.
但是目前关于谱正Lévy过程的最优分红与注资问题的研究相对较少,谱正Lévy 风险模型中分红与注资策略同时优化的一些问题尚未解决.基于前人对于此问题的研究,本文研究带比例交易成本的Lévy风险模型中的最优分红和注资问题,其中分红只能在独立泊松过程的跳跃时间下进行.假设Lévy风险模型中分红策略是周期障碍策略,通过构造q-尺度函数求解最优策略和值函数,并运用验证定理证明周期障碍策略的最优性.
1 模型建立
1.1 谱正Lévy过程
设X={Xt}t≥0是定义在完备的带流概率空间(Ω,F,F,P)上有非单调轨迹的谱正Lévy过程,其中F={Ft}t≥0是由随机过程X生成的,谱正Lévy过程意味着没有负跳.

(1)
其中1A表示集合A的示性函数.假设-ψ′(0+)=E(X1)>0,即随机过程X趋于+∞.随机过程X是有界变差的充要条件是
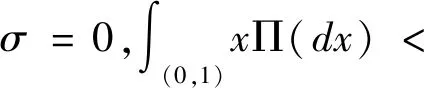
此时,公式(1)可写为
(2)
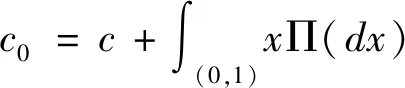
1.2 泊松分红策略下的最优控制问题
假设一个公司的盈余过程由Lévy过程X驱动,其中拉普拉斯指数见公式(1).控制策略分为分红和注资两部分.给定一个策略π,记Lπ表示分红策略,Rπ表示注资策略.假设分红是周期分红策略,此时假设分红只能在到达时间T=(T(i);i≥1)进行,其中分红时刻是由强度r>0的独立泊松过程Nr=(Nr(t);t≥0)所决定.
对于分红过程,Lπ的形式为
(3)
其中νπ关于由过程(X,Nr)所生成的域流F=(Ft)t≥0是适应的.
对于注资过程,假设Rπ是非递减、右连续的,适应F过程且满足Rπ(0)=0.与分红相反,资本注入可以持续进行,相应的盈余过程记为
Uπ(t)=X(t)-Lπ(t)+Rπ(t),t≥0.
设Π表示可允许策略的集合,定义破产时刻为Tπ=inf{t>0:Uπ(t)<0}.令inf ∅=∞.
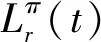
(4)
本文的目的是计算值函数

与此同时,在策略存在的情况下找到与其对应的最优策略π*∈Π.
2 周期障碍策略
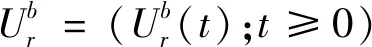

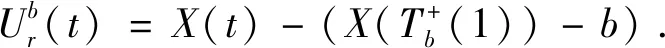
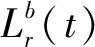
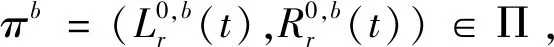
(5)
2.1 尺度函数
预期红利净现值可以通过波动理论计算,为了使得求解的预期红利净现值公式(5)最大.下面给出尺度函数的定义及其相关性质.
定义1 固定q≥0,函数族W(q)(x)满足:[0,∞),当x<0时,W(q)(x)=0;当x≥0时,存在非负连续严格递增的函数W(q)(x),其拉普拉斯变换为
(6)
其中ψ如公式(1)所定义,且
Φ(q)=sup{θ≥0:ψ(θ)=q},
(7)
则称函数族W(q)(x)是q-尺度函数.
类似文献[14]中的定义2,可定义与W(q)(x)相关的伴随尺度函数Z(q)(x):[1,∞),
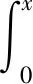
当x∈,同样定义下面的函数
注意,当-∞ (8) 下面得到关于W(q)(x)的一些性质[15]: 如果随机过程X是有界变差,则对任意q≥0,W(q)|(0,∞)∈C1(0,∞)的充要条件是Π没有原子;如果随机过程X是无界变差,则对任意q≥0,W(q)|(0,∞)∈C1(0,∞).此外,如果σ>0,则C1(0,∞)可以替换为C2(0,∞).如果Lévy测度有密度,则尺度函数始终是可微的[16],可以得到W(q)(x)和W(q)′(x)的初值 (9) 利用W(q)(q+r)和Φ(q+r),是由公式(6)和公式(7)中用q+r代替q定义的.根据ψ在(0,∞)上的凸性,可得当r>0时,有Φ(q+r)>Φ(q).当q,r>0,x∈时,令 (10) 对公式(10)关于x求偏导,得 Z(q)′(x,Φ(q+r))=Φ(q+r)Z(q)(x,Φ(q+r))-rW(q)(x),x>0. 同样,定义 (11) 则 (12) 下面运用上述的尺度函数来计算预期净现值式(5). 引理1 对于所有的b≥0,x≥0,有 (13) 证明首先利用文献[17]中推论3.3和推论3.4可得 (14) (15) 由公式(14)与公式(15)可得 注1 当x>b>0时,公式(13)为 本节首先确定候选障碍值b*,其次证明在b处满足光滑性的条件,最后证明最优障碍值b*的存在性. 定理1 在b处满足期望的光滑性条件是 (16) 证明对于所有的b>0,x∈(0,∞){b},对式(13)求导,可得 (17) 当x>b时,可得 (18) 首先,当b>0时,Vb是连续可微的,可得 接着,对Vb求二阶导,有 因此,要使Vb二阶可导,可得 显然,二次连续可微性对于无界变差情形自然成立,但是对于有界变差情形时当且仅当满足式(16)才成立. 最后,对于无界变差情况,考虑函数Vb的三阶导数的连续性.运用公式(9)、(17) 和(18),得 如果 则值函数Vb有连续的三阶导数,值函数Vb三阶导数连续当且仅当满足条件公式(16). 下面证明b*的存在性,使得条件Cb对于b=b*成立. 引理2 公式(16)存在唯一解b>0当且仅当 (19) 证明满足公式(16)等价于满足h(b)=0,其中 (20) 对公式(20)求导,得 因此,公式(16)存在唯一解b使得h(b)=0当且仅当h(0)<0,根据公式(19)可知 根据引理2,若公式(19)成立,则取公式(16)的唯一根作为候选最优障碍值b*. 下面证明周期障碍策略πb*的最优性.对于b*>0,由于b*满足Cb,所以公式(13)的预期净现值可以简写为 (21) 当b*=0,得 (22) 下面将提供验证引理并证明Vb*满足公式(16).给定一个可测函数g是充分光滑的,如果g是(0,∞)上连续可微的函数族(相应C2(0,∞)表示(0,∞)上的二次连续可微的函数族),则X具有有界变差(相应无界变差)路径.令L是作用于充分光滑函数g上的算子,可表示为 (23) (24) 下面将证明候选值函数Vb*满足公式(24).根据引理4.2[7],可知Vb*是足够光滑的. 证明(i) 假设b*>0,由(16)式和(17)式,对于所有的x>0,可得 (25) 在b*点处的二阶导数 (ii)假设b*=0, (26) 当x>0时,对公式(26)求导得 (27) (28) 特别是 (29) 则V0′(0+)≤α. 引理5 当b*>0时, (30) 引理6 当b*>0时, (31) 当b*=0时,有 (32) 证明假设b*>0,利用文献[18]中定理2.1,可得 (L-q)K(q,r)(b*-x)=0,0 (33) 利用文献[19]中(3.9)式和(3.10)式,对于任意的0 (34) (L-q)Z(q,r)(b*-x,Φ(q+r))=0,0 (35) (L-q)Z(q)(b*-x)=0,0 (36) (i)当0 (37) 可得 (ii)当x>b*时, (38) (39) 可得 特别是,当b*=0时, 定理2 周期障碍策略πb*是最优的,并且对所有的0≤x<∞,值函数V(x)=Vb*(x). (i)假设b*>0.当x≤b*时,引理5和引理6说明了公式(24)等号成立.当x>b*时,将公式(21)带入公式(30)中,得 (ii) 假设b*=0.将公式(22)带入公式(30),得 将上式和公式(32)结合,即得公式(24)等号成立. 本文研究了带比例交易成本的Lévy风险模型中分红只能发生在独立泊松过程跳跃时刻约束下的最优分红和注资问题.将分红与注资同时优化,通过构造q-尺度函数来求解最优策略和值函数.本文假设分红策略是周期障碍策略,找到一个候选障碍值b*并证明其存在性.最后,运用验证定理证明了周期障碍策略的最优性,从而解决了带比例交易成本的Lévy风险模型中的最优分红和注资问题.
2.2 计算预期净现值

3 候选最优障碍值b*的选择
3.1 平滑拟合
3.2 b*的存在性

4 最优性验证
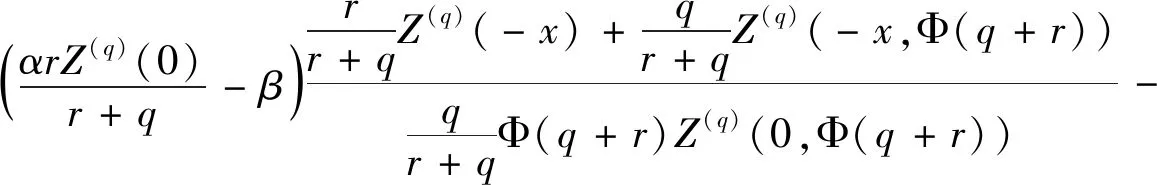





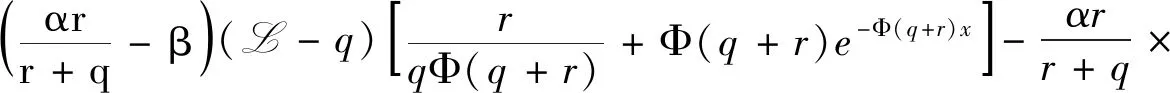
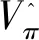
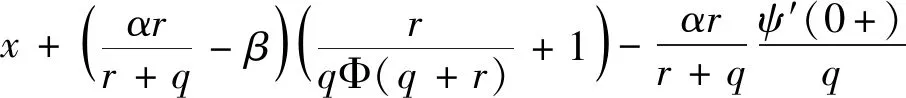
5 结束语

