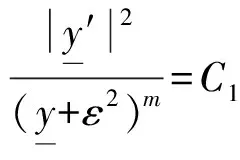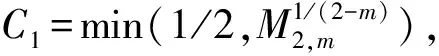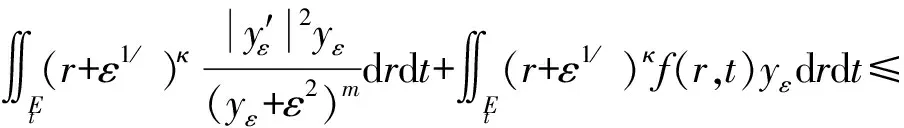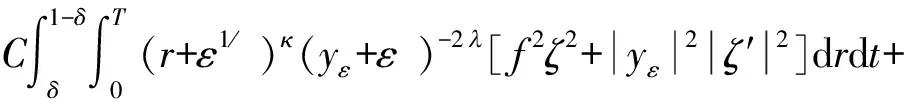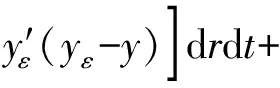一类含梯度项的奇异抛物型方程弱解的存在性
张亚茹, 夏 莉,2*
(1. 广东财经大学统计与数学学院, 广州 510320; 2. 广东财经大学大数据与教育应用统计实验室, 广州 510320)
含有梯度项的奇异抛物方程可以描述热化学反应、人口动态学、非牛顿流体、渗流现象和相变理论等领域中的许多实际问题。这类含梯度项的奇异抛物方程可能出现多处奇性项和非线性项,从而造成理论研究上的本质性困难。而且,这类奇异方程在一定条件下可以通过某些变换转化为其他类型的方程。因此,对于带梯度项的奇异抛物型问题的解的研究一直是热点问题。
在过去的几十年里,学者们获得了许多有关含梯度项奇异抛物方程的理论成果。例如,假设f(|x|,t)是径向对称函数,A1为N(N≥2)中的单位球,学者们研究了
(1)
的非径向经典解或弱解的存在性、唯一性和渐近行为[1-3];讨论了与方程(1)相关的一些奇异椭圆方程,得到了其正则化的结果,并证明了这些奇异椭圆方程的非负弱解的存在性、唯一性[4-8]。
其次,当用p-laplace算子Δpy=div(|∇y|p-2∇y)(p>1)代替方程(1)中的算子Δy时,学者们研究了这类非线性抛物方程或椭圆方程的解的存在性和唯一性[9-10];考虑了某些非线性抛物方程边值问题的非负解的存在性[11];进一步考虑了某些含超线性奇异梯度项的抛物型方程Cauchy-Dirichlet问题的非负解的存在性[12]。
此外,如果定义|x|=r,则方程(1)转化为方程

(2)
的初边值问题,其中,y≥0,(r,t)(0,1)×(0,T]。在l=2时,ZHOU和LEI[13]研究了当κ=0,1≤m<2时,问题(2)的经典正解的存在性;ZHOU[14]研究了在1≤m<2的情况下,与问题(2)相关的奇异椭圆边值问题存在正解的充分条件;夏莉和李敬娜[15]考虑了问题(2)在m=1的特殊情况下的弱解。在l>0时,XIA和ZHANG[16]研究了问题(2)的古典解的存在性。
本文主要研究以下含梯度项的奇异抛物型方程
的弱解,其中,κ≥0和λ>0都是常数,m(0,2),f(r,t)、φ(r)是分别满足条件(H1)、(H2)的函数:
(H1)f(r,t)且在上f(r,t)>0;
(H2)φ(r)C(0,1)∩H1(0,1),在区间(0,1)中,φ(r)>0,且φ(0)=φ(1)=0。
本文使用抛物正则化法和上下解方法,研究了0 为了得到问题(3)~(5)的解,约定: (D3)区间[0,T]中,g(t)为C1连续函数,且满足函数值g(t)≥1和一阶导数g′(t)>0; G(s)=sm-1-1(λ+-1)·[max[0,T]g(t)]m-1+ sm-2-2·maxETf·[min[0,T]g(t)]m-2。 其次,除了f(r,t)、φ(r)(分别简记为f、φ)需要满足的条件(H1)、(H2)外,还需要给定以下条件: (H3)当κ>0,λ>(κ+1)/2时,有 C12g(0)(1-r2) (H4)当κ[0,1],λ>0时,有 C12g(0)(1-r2) 上述条件中C1、C2、C3均为常数,C1<1/2,C2,C3≥1。 下面对问题(3)~(5)的弱解进行定义。 定义1如果函数y≥0,且满足以下条件: (i)在ET上,y几乎处处大于0; (ii)y且有ytV*及rκ|y′|2L1(ET); (iii)对于任意函数Ψ以下等式成立: 则称y为问题(3)~(5)的弱解。 下面将问题(3)~(5)进行正则化,同时给出正则化问题的古典上下解定义。 显然,在r=0和y(r,t)=0时,方程(3)具有奇异性。故需要对问题(3)~(5)进行正则化,将其转化为以下正则化方程 (6) 由条件(H1)、(H2)及文献[17],容易得到问题(6)的古典解yε的存在性。为了后续证明过程中表述的简洁,给出以下简记符号: F(ξ)=ξt-ξ″, 令y0=g(t)(r-r2)/2,其中g(t)满足条件(D3)。显然,y0为以下问题的古典解: 其中,b(r,t)=g′(t)(r-r2)/2+g(t)。显然,在ET上有0≤y0≤rg(t),并且对∀δ(0,1/2),在[δ,1-δ]×[0,T]上有y0>0。 定义2若在ET中y≥0几乎处处成立,yV,ytV*,且对∀0≤ΨV,均有 则称y为问题(6)的弱下解。同理,将上述符号反号,可得其弱上解的定义。 首先引入以下引理。 证明由问题(6)可得 f(r,t)≤C1 引理2假设κ>0,λ>(κ+1)/2,且条件(H3)成立,令y1ε=C2g(t)(r+ε1/),y2ε=C2g(t)(1+ε1/-r),其中,δ(0,δ0),0<δ0<1/2,则是问题(6)的古典上解。 F(y1ε)-hε(r,t,y1ε,y′1ε)=C2g′(t)(r+ε1/)- C2(κ+-1)g(t)(r+ε1/)+ -C2(κ+-1)g(t)(1+ε1/)+ -C2(κ+-1) 其中, Sε(t)=C2(κ+-1)g(t)[1-(1+ε1/)]+ 又因为g(t)和g2-m(t)在[0,T]上一致有界,故对∀t[0,T],当ε→0时,易证Sε(t)→0。 受文献[14]的启示,易知存在正常数C2≥1,使得G(C2)<λ,其中函数G(s)已由条件(D4)给出。因此,当0 F(y1ε)-hε(r,t,y1ε,y′1ε)≥ 当1 F(y1ε)-hε(r,t,y1ε,y′1ε)≥ 其中,L=(λ+-1)/。这表明对∀ε(0,δ0),(r,t)ET,F(y1ε)-hε(r,t,y1ε,y′1ε)≥0。同理可证F(y2ε)≥hε(r,t,y2ε,y′2ε)。证毕。 引理3假设κ[0,1],λ>0且条件(H4)成立,令其中则是问题(6)的古典上解。 证明显然,zε是如下问题的古典解: (7) f(r,t)(r+ε1/)κ≥C3g(t)-f(r,t)(r+ε1/)κ, 由引理1至引理3和问题(6)的最大化原理,可得在ET中 (8) 几乎处处成立。 引理4对∀ε(0,1),t(0,T],(r,t)Et,有 其中,Et=(0,1)×(0,t],C是与ε无关的正常数。 证明由 ∬Et(r+ε1/)κ(F(yε)-hε(r,t,yε,y′ε))yεdrdt=0 可得 ∬Et(r+ε1/)κf(r,t)yεdrdt。 由式(8)可知 其中,C是与ε无关的正常数。证毕。 下面给出∂yε/∂t的局部估计。 引理5对所有的ζ(0,1),∀t(0,T],有 ∬Et[(r+ε1/)κ(yε+ε)-2λ|yεt|2ζ2]drdt+ 其中,Et=(0,1)×(0,t],δ(0,1/2),Cδ是仅与δ相关的正常数。 证明令 则uεt=(yε+ε)-λyεt,u′ε=(yε+ε)-λy′ε,故式(6)可以写为以下形式: (r+ε1/)κuεt-((r+ε1/)κu′ε)′=(r+ε1/)κ(yε+ε)-λf(r,t)。 首先,考虑等式 ∬Et[(r+ε1/)κ[|uεt|2-(yε+ε)-λf(r,t)uεt]- ((r+ε1/)κu′ε)′uεt]ζ2drdt=0。 (9) 注意到式(9)中 -∬Et((r+ε1/)κu′ε)′uεtζ2drdt= (10) 因为ζ故∃δ(0,1/2),使得在(0,1)[δ,1-δ]上,ζ≡0,ζ′≡0。再采用与参考文献[18]相似的方法,由式(9)、式(10)、Hölder不等式和Young不等式可得 ∬Et(r+ε1/)κ(yε+ε)-2λ|yεt|2ζ2drdt+ 因此 ∬Et(r+ε1/)κ(yε+ε′)-2λ|yεt|2ζ2drdt+ 证毕。 引理6对∀ε(0,1),∀r1,r2[δ,1-δ]和∀t1,t2[0,T],有 |yε(r2,t2)-yε(r1,t1)|≤C1δ|r2-r1|1/+C2δ|t2-t1|1/2, 其中,δ(0,1/2),C1δ、C2δ仅与δ有关,且C1δ为非负常数,C2δ是正常数。 (11) 由引理5,可得 取Δt=|t2-t1|,使得r1+Δt1/[δ,1-δ]。由引理5、Hölder不等式和Young不等式,可得 (12) 其中,k()=(2+)/(2+-1)。 再结合式(12)可得 |yε(r,t2)-yε(r,t1)|≤C2δΔt1/2。 最后,由式(11)可得 |yε(r2,t2)-yε(r1,t1)|≤C1δ|r2-r1|1/+C2δ|t2-t1|1/2, 证毕。 yε→y,(r,t)ET; (13) 在L2(ET)中,有 y′ε⇀y′; (14) (15) 式(14)、(15)中“⇀”表示弱收敛。 从引理4和Lukin定理可知 (16) 引理7对∀ζ当ε→0时,有 ∬Etrκ+1ζ2||y′ε|2-|y′|2|drdt→0。 证明 ∬Etrκ+1ζ2(yε-y)(F(yε)-hε(r,t,yε,y′ε))drdt=0, 将其展开后可得 ∬Etrκ+1ζ2y′ε(yε-y′)drdt+∬Etrκ+1ζ2(yε-y)yεtdrdt+ ∬Etrκ+1ζ2(yε-y)f(r,t)drdt=0。 (17) 当ε→0,采用类似文献[18]的方法,由引理4、引理5、Hölder不等式和Lebesgue控制收敛定理,可得 I1=∬Etrκ+1ζ2(yε-y)yεtdrdt→0, I2=∬Etrκ+1y′εζζ′(yε-y)drdt→0, 已知ζ且在C((0,1)×[0,T])上,yε一致收敛到y,则由式(8)、引理4和Lebesgue控制收敛定理,当ε→0时,可得 I4=λ∬Etrκ+1ζ2(yε+ε)-1(yε-y)|y′ε|2drdt≤ (18) 由式(18)和式(16),当ε→0时,有 ∬Etrκ+1ζ2y′ε(yε-y)drdt→0。 由式(13),当ε→0时,有 ∬Etrκ+1ζ2y′ε(yε-y)′drdt→0。 因此 ∬Etrκ+1ζ2|y′ε-y′|drdt→0。 最后,在V*中,由式(15)和引理4,可得 ∬Etrκ+1ζ2||y′ε|2-|y′|2| drdt≤ 证毕。 注1在证明引理7的过程中,可以进一步证得问题(3)~(5)的弱解yC((0,1)×[0,T])。 本文主要结论如下: 定理1令κ>0,λ>(κ+1)/2,假设条件(H1)、(H2)成立,且函数φ满足条件(H3),则问题(3)~(5)至少存在一个弱解。更进一步,∀t[0,T],有y′(0,t)=y′(1,t)=0。 接下来,仍采用文献[18]类似的方法,易证y满足定义1中的条件(iv)。 此外,由式(8)得 C1g(t)(r-r2)≤y(r,t)≤ C2g(t)·min{r,(1-r)}((r,t)ET)。 从而 因此,y′(0,t)、y′(1,t)存在且y′(0,t)=y′(1,t)=0,t(0,T]。证毕。 定理2令0≤κ<1,λ>0,假设条件(H1)、(H2)成立,并且函数φ满足条件(H4),则问题(3)~(5)至少存在1个弱解。 定理2的证明过程类似定理1,在此略。 最后,给出问题(6)的弱比较原理: 定理3令κ>0,λ>0,假设y1、y2分别为问题(6)的弱下解和弱上解,如果在(0,1)内y2(r,0)≥y1(r,0)几乎处处成立,且在(0,T)内y2(0,t)≥y1(0,t),y2(1,t)≥y1(1,t)几乎处处成立,则在ET上y2≥y1几乎处处成立。 证明由弱下解和弱上解的定义可得:对∀ΨL2有 f(r,t)Ψ]drdt≥0, (19) f(r,t)Ψ]drdt≤0, (20) 其中,Et=(0,1)×(0,t],t[0,T]。 定义函数ρ(s):(0,∞)→为 其中,若m(0,1),则令am=0;若m≥1,∃c1,c2>0,使得yi≥ci(i=1,2)成立,则可取am=min(c1,c2)。 注意到 且 可得 通过以上变换,式(3)转换为 故不等式(19)、(20)分别可变为 ∬Et{[ρ(y2)]tΨ+[ρ(y2)]rΨ′-[ρ′(y2)]f(r,t)Ψ- (21) ∬Et{[ρ(y1)]tΨ+[ρ(y1)]rΨ′-[ρ′(y1)]f(r,t)Ψ- (22) 记w=ρ(y1)-ρ(y2)=(ρ1-ρ2),再由式(22)减去式(21),可得 ∬Et{wtΨ+wrΨ′+[w′(y2)-w′(y1)]f(r,t)Ψ- 同时,注意到Ψ=(w)+其中(w)+=max{0,w},则有 在[am,∞)中,w′≥0且w″≤0,所以,在ET中 [w′(y2)-w′(y1)]f(r,t)w+≥0 几乎处处成立。 又因为y′1≤y′2,故 综上可知 由此可得,在ET上w+=0几乎处处成立,故在ET上y2≥y1几乎处处成立。证毕。1 预备知识






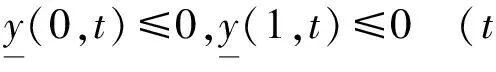


2 主要结论及其证明