斜拉桥面内多重内共振下索-梁-索耦合效应的数值研究

陈柯帆，李 源,2，贺拴海,2，王 康，卓鸿杰，宋一凡,2

(1.长安大学公路学院，陕西，西安 710064；2.长安大学旧桥检测与加固技术交通行业重点实验室，陕西，西安 710064)

斜拉索作为大跨径斜拉桥的主要承力构件，与主梁、桥塔等构成的缆索体系结构整体柔度大、刚度小，存在拉索的局部模态，亦存在结构的整体模态，具有复杂的非线性动力行为[1]。当外荷载作用于桥梁结构上时，结构的整体模态运动将通过拉索锚固端对其运动产生周期性的间接激励。若局部-整体模态频率满足一定比例关系[2]，微小的外激励也将引起结构发生剧烈内共振行为[3-4]。迄今已在多个国家实桥中监测到具有此特征的拉索剧烈振动，为桥梁的安全运营带来了极大风险[5]。

较风雨[6-7]、车桥耦合[8]等直接激励引起的全桥振动而言，间接激励作用下的斜拉桥内共振行为致振因素更多、更隐蔽，引起了国内外学者的广泛关注。传统依托有限元软件建立数值模型分析缆索结构的非线性振动问题具有较高局限性，需要深度优化索单元及其数值分析方法[9-12]以缓解低效率问题。WARNITCHAI 等[13]、MACDONALD等[14]、GATTULLI 等[15]、孙测世等[16-17]和吴庆雄等[18]先后进行了动力试验，观测到斜拉索局部模态与结构整体模态耦合产生的丰富内共振行为，其试验结果为建立更精细化斜拉桥整体动力学模型提供了重要参考。在理论研究方面，由于斜拉桥结构的复杂性，以及非线性动力学研究方法对于多自由度问题的局限性，现有学者只能基于不同研究目的，建立能够解释斜拉桥部分动力行为产生机理的简化模型。其中，康厚军等[19-22]通过建立主梁的传递矩阵，针对多索-梁结构[19]、悬索结构[20]、多索-拱[21-22]进行了深入的理论研究，讨论了索力、二次项系数等参数对于结构共振特性的影响；诸俊[23]通过回传射线矩阵法求解了双索-梁的动力学模型的振动方程，分别研究了支点变化位移作用、拉索损伤等因素对结构非线性振动特性的影响；CAO 等[24]通过建立主梁的分段函数，将主梁依拉索等效为若干独立梁段并通过拉索锚固处的边界条件对不同子系统的振动方程进行求解，得到了斜拉桥四索系统的常微分方程组；GUO 等[25]建立了双水平索-塔的动力学模型，研究了塔的扭转效应对结构参数振动的动力行为影响；孙测世等[26]建立了带辅助索的长索振动模型，研究了减振方法。

当前，斜拉桥跨径越建越大，拉索也越来越长，且多为密索、对称布置。其中，相邻或对称的拉索局部模态频率数值上相近，而短索和长索的局部频率也可能同时与结构相邻两阶竖向频率满足“1∶1”的比例关系。在这两种情况下，多根拉索的局部模态将同时与结构的整体模态耦合而产生多重“1∶1”内共振。此时共振的拉索将通过桥面改变另一根拉索的动力特性，或将进一步加剧结构振动[16-17,27]。因此，研究此索-梁-索耦合效应对开展精细化分析并有效避振非常重要。然而，除少量文献[27]外，目前鲜见针对此耦合效应的理论研究。现下仍存在着大量理论无法解释试验、试验无法指导设计现象，对于斜拉桥整体动力学建模理论与分析方法仍有待更深入的开展[28]。

为研究斜拉桥多重内共振下的索-梁-索耦合效应变化规律，本文通过离散主梁参数质量体系建立了新的斜拉桥面内整体动力学模型。该模型考虑了多索的几何非线性、主梁变截面和变弯曲刚度影响、拉索间振动影响作用，通过有限差分法修正了斜拉桥面内运动模型的振动微分方程组，依托4 阶～5 阶Runge-Kutta 积分方法对方程组进行了数值仿真，讨论了在局部-整体模态耦合发生多重“1∶1”内共振下的索-梁-索耦合效应问题。本文提出的斜拉桥整体动力学模型更加精细，研究结果可为斜拉桥设计提供参考。

1 基于索-梁结构的斜拉桥面内整体动力学模型

1.1 主梁集中质量参数体系与结构整体构型

为模拟具有分布质量的变截面主梁在多截面轴力、多点弹性支承作用下的动力行为，不考虑主梁纵向运动对振动的影响，将主梁按等间距离散为集中质量参数体系，如图1 所示。

图1 主梁参数质量体系简化过程Fig.1 The reduced process of the integrated dynamic system composed of lumped-mass beam segments

图1 中各独立梁段两侧存在剪力与轴力作用，可在离散参数体系中模拟连续主梁的弯曲刚度作用。在多数斜拉桥实际工程中，各斜拉索锚固点处附近的主梁单独设有横向连接，其截面参数与主梁的其他截面不同。因此，定义E1和I1表示未与拉索相连的无索区梁段的弹性模量与竖向弯曲惯性矩；E2和I2表示有索区梁段的弹性模量与竖向弯曲惯性矩。在此基础上，考虑斜拉桥塔为刚性桥塔，将主跨为120 m 的斜拉桥主梁按照2 m 1 个节段(r=2 m)划分为59 个独立梁段(1≤j≤59,J=59)，其中简支边界下起点和终点梁段无竖向位移，忽略其质量后从左至右依次编号并定义为B1#～B59#，建立八索-变截面梁的动力学模型如图2 所示，各拉索锚固点坐标如表1 所示。

表1 拉索锚固坐标Table 1 The anchored coordinate of cables

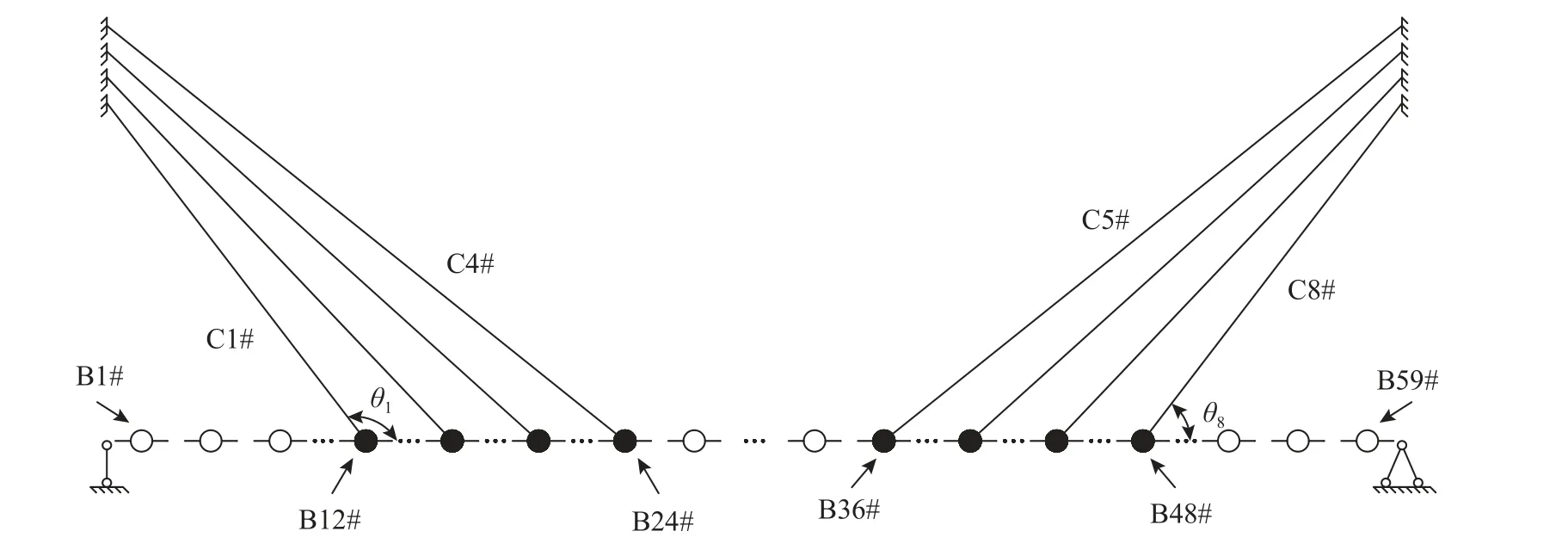
图2 基于离散化主梁参数质量体系的斜拉桥面内整体动力学模型Fig.2 The in-plane global vibration model of a cable-stayed bridge established based on the integrated dynamic system composed of lumped-mass beam segments

本文约定下标“c、b”分别为索、梁的相关参数；i和j分别为对拉索和梁段的计数，定义“Ci#”和“Bj#”分别为第i根拉索和第j个梁段；定义xbj为主梁纵向坐标；θci为拉索与主梁大里程方向夹角。

1.2 索、梁微元段受力分析

取图2 中拉索的微元段受力示意图如图3 所示。

图3 拉索微元段受力示意图Fig.3 The force diagram of Ci# in the dynamic state

图3 中：Tin为拉索微元段起始点处的切向动索力，由式(1)定义；xci为拉索弦向坐标；yci为拉索横向坐标；mci为Ci#沿xci的单位长度质量；aci为Ci#在yci方向上的加速度；g为重力加速度，本文中取9.8 m/s2。假设拉索质量沿轴向均匀分布[27,29-30]，根据拉索微元段在yci方向的平衡关系，由达朗伯原理可得到拉索微元段的振动平衡方程[1,9,20,29-30]：

式中：sci为Ci#的动态弧长；Tci和τci分别为Ci#切向的初始索力和动索力增量；uci、vci、wci简写自uci(xci,t)、vci(xci,t)、wci(xci)，其中uci(xci,t)为拉索在xci方向的振动位移，vci(xci,t)为拉索在yci方向的振动位移。由于拉索的横向振动相对于整体而言仍属于微小运动，且若仅考虑拉索的低阶振动模态，拉索的横向与纵向振动模态间不存在相互作用[31]，因此忽略拉索的纵向惯性力作用，并将拉索轴向与切向几何关系作如下简化[32]：

式中：Hci和hci分别为Ci#在xci方向的初始索力和动索力增量； εci为平均动应变； ε0ci为初始平均动应变；Uci为Ci#在xci方向的伸长量； Δsci为相对于初始状态的弧长动增量。

式中：Li为Ci#上下锚固点在xci方向上的距离；Lci为Ci#的静态长度；Dci为Ci#中点处的垂度：

因此，拉索振动时，轴向拉力的单位动增量为：

式中：Eci和Aci分别为Ci#的弹性模量及横截面积。将式(7)在xci方向积分，可得拉索振动的轴向动拉力表达式为：

拉索振动时，其下端与Bji#运动关联，以主梁竖直向上、拉索弦向顺时针为推导正方向，则拉索边界条件为：

式中：Vbj(t)为Bj#振动时与时间相关的形状变化因子，另有Vci(t)表示Ci#振动时与时间相关的形状变化因子，并将Vci(t)和Vbj(t)简写为Vci和Vbj；vbj(xbj,t)为Bj#的竖向位移表达式，按照本文的主梁集中质量参数体系简化方法，Bj#的竖向位移即为Vbj。将式(9)～式(11)代入式(5)～式(8)，积分、化简后同式(3)～式(4)代入式(2)，消掉索力轴向平衡多项式，可得拉索振动方程：

式中：“′”为对轴向坐标的偏导；“·”为对时间的偏导。为得到Bj#的运动方程，取图2 中有索区梁段竖向运动的受力示意图如图4 所示。

图4 有索区主梁微元段受力示意图Fig.4 The force diagram of Bji# in the dynamic state

无索区梁段与有索区梁段的受力区别仅与索力相关，根据狄拉克函数δ 的性质，依据达朗伯原理和图4 对Bj#进行受力分析：

式中：γb(j-1,j)为Bj-1#和Bj#面内运动的转角；Fb(j-1,j)与Fb(j,j+1)、Nb(j-1,j)与Nb(j,j+1)分别为Bj#左、右侧剪力与轴力。依据梁段间微元段左侧弯矩平衡可得：

式中：Mbj为主梁在Bj#位置处的弯矩。假设分段足够密集，可采用差分法对Bj#处位移偏微分方程及几何关系进行简化[30,32-33]：

无索区梁段左右侧轴力大小相等，方向相反，如式(19)；有索区梁段左右侧轴力差为该拉索索力的水平分力，由于索力动增量相对于整体较小，因此主梁轴力仅考虑初始索力，如式(20)。

图4 中主梁左右侧为简支端，其边界条件为：

式中，“e-、e+”分别为主梁左、右侧边界。假设振动发生前系统处于平衡状态，消掉重力式后，将式(15)～式(22)代入式(13)可得Bj#主梁的竖向振动方程：

式中，因假设主梁不同截面存在不同弯曲刚度特性，因此EbjIbj对Bj-1#和Bj+1#的振动皆有交互的影响作用，如式(23)中的第3 个～第7 个多项式所示。对于不同结构体系的斜拉桥，需根据实际结构修正式(21)和式(22)，在求得新的B1#与BJ#运动方程后可得该结构的面内整体运动方程。

1.3 斜拉桥面内整体动力学模型的运动方程

为便于找到斜拉桥的内共振形式，采用拖拽法定义构件在第k阶整体模态下的振动位移表达式为[34]：

式中：φci(xci)(k)与φbj(xbj)(k)分别为Ci#与Bj#在第k阶整体模态下的振型表达式；fci(xci)为与梁振动形态和结构几何边界条件相关的模态拖拽函数，定义其基本形式为[32,34]：

采用满足斜拉索力学和几何边界条件的三角函数作为其振型基函数[18,29]，如式(26)；构造拉索面内横向一阶振动位移表达式如式(27)[1,9,20,29,32]：

由于张紧弦的自由振动，低阶基本模态占据主要地位[35]。为简化计算，本文仅考虑拉索的一阶局部模态，即取式(27)中k=1，连同将式(25)代入式(12)，并应用Galerkin 方法进行拉索的1 阶模态截断，整合式(23)后可以得到图2 所示系统的面内自由运动方程组：

式中：A为剪力影响矩阵，表征了图1 中离散化的主梁参数系统振动时受到的来自于不同拉索的间接影响和主梁弯曲刚度影响；D为轴力影响矩阵，表征了主梁参数系统振动时受到的不同索力水平分力影响。式(29)和式(30)展开后为定义了结构面内自由运动的常系数齐次微分方程组，其中加粗符号表示矩阵，各多项式系数具体形式列于附录1。

此外，从动力方程整体看，在多重内共振发生时， Ci#振动将影响Bji#振动，而由于剪力和轴力作用，Bji#的振动将影响Bji+1#，进而影响Ci+1#，因此振动时索-索间的相互影响效应将通过主梁的剪力、轴力效应进行传递，即式(29)和式(30)反映了多重内共振下的索-梁-索耦合效应。

2 面内振动模态的特征值解法

基于式(29)和式(30)行列式关系，构造系统的固有振动特征根方程[36]：

式中：下标“N” 的参数表示结构面内固有振动模态参数，定义“Nk”表示结构面内第k阶固有振动模态参数；另有 “Vk”结构面内第k阶竖向固有振动模态参数；TN为结构特征对角矩阵，由式(32)定义；VN为结构各构件形状变化因子的对角矩阵，由式(33)定义：

式中，Ωci与Ωbj分别为拉索和主梁质点系的局部模态特征对角矩阵，其对角元素Ωci与Ωbj分别为Ci#和Bj#局部模态的振动频率：的超越方程，对TN进行特征值求解可得结构

式(32)中的TN实际是关于系统固有振动频率的模态参数：

3 算例模态分析

3.1 基础工况参数

本文的基础工况(简称CC1)算例参数参考自西北地区一座三跨、双塔混凝土斜拉桥，其中主梁参数如表2 所示，拉索参数如表3 所示。

表2 主梁参数取值(CC1)Table 2 The parameters of the main beam under CC1

表3 拉索参数取值(CC1)Table 3 The parameters of cables under CC1

3.2 模态分析与验证

采用商业有限元软件(MIDAS/CIVIL)对3.1 节中CC1 算例进行有限元建模，其中拉索用桁架单元模拟，初始索力用桁架单元内力输入；主梁用梁单元模拟。两种单元长度皆为1 m。采用子空间迭代法对自重作用下的结构进行面内模态特征分析。汇总有限元方法(简称FEM)与本文方法(简称ASM)得到的结构N1 阶～N5 阶模态振型如图5所示。

图5 两种方法得到的结构前5 阶固有振动模态振型对比图Fig.5 The natural modal shapes of the first-5 orders obtained by these two methods

如图5 所示，本文方法计算得到的振型结果与有限元计算结果较吻合。图5 中，结构前3 阶模态的模态局部化参数 ΛB[16,24,37]超过了80%，是结构的V1 阶～V3 阶整体模态。根据此汇总两种方法得到V1 阶～V10 阶整体模态频率值如表4 所示。

表4 中两种方法得到的结构V1 阶～V10 阶模态频率计算结果最大误差为3.2%，平均误差为1.4%，进一步验证了本文方法适用性与准确度。

4 数值解析与讨论

4.1 竖向模态激励作用下的“拍”振现象

采 用 4 阶～5 阶 Runge-Kutta 方 法， 运 用MATLAB/SIMULINK 建立了数值仿真模型，计算基础步长为0.001 s，在跨中(B30#)增加0.1 m 的竖向初始挠度，不考虑结构阻尼作用，运行200 s后可以得到C1#～C8#的振动响应图如图6 所示。

图6 中可以清晰观测到，在CC1 工况条件下，无拉索产生明显的耦合内共振。引入系数χci表示Ci#拉索局部频率(Ωci)增量，由式(37)定义；为Ci#拉索局部频率与结构竖向第k阶模态频率()的靠近程度，由式(38)定义[24,32]：

改变χci即可调整Ci#的局部模态频率值(Ωci)至与结构的第k阶整体模态频率满足“1∶1”比值关系，使得=0。在CC1 基础上，将初始激励减小为1 cm，设定2#工况：

1) 2-1#工况(CC2-1)：改变χc3值使得=0，此时Ωc3=，运行时长为200 s。

2) 2-2#工况(CC2-2)：改变χc5值使得=0，此时Ωc5=，运行时长为200 s。

运用快速傅里叶变换方法(简称为FFT)分别对C3#和C5#振动响应进行分析，各拉索振动响应图如图7(a)～图7(b)所示，其频谱图如图7(c)～图7(d)所示。

图7 CC2#工况条件下，拉索响应图与频谱图Fig.7 The response and spectrogram of cables under CC2#

图7(a)和图7(b)中，C3#和C5#产生了鲜明的耦合“拍”振，振动位移也远大于图6 中响应曲线数值。从对应图7(c)和图7(d)可以看到，C3#和C5#此时分别与竖向第5 阶模态和竖向第3 阶模态发生了“Ωc3∶=1.82∶1.8233”、“Ωc5∶=0.795∶0.7843”的“1∶1”内共振。研究表明[38]：“拍”频内共振的存在完全是由系统的非线性动力特性决定的，其非线性项系数对内共振影响较大[39]。因此，图7 结果也进一步验证了本文提出的动力学模型能有效模拟结构的非线性动力行为。

4.2 与不同阶整体模态耦合时的索-梁-索耦合效应

研究表明[32]：外部激励施加于主梁产生的结构面内整体模态，与该作用点处对应的振型参与系数密切相关。若在跨中处施加初始振幅激励，由于该作用点处偶数阶振型的振型参与系数数值上为0，则无法激励主梁产生偶数阶模态。为避免上述干扰，研究多索与不同阶竖向模态耦合时的索-梁-索耦合效应，基于CC2 工况设置3#工况条件如下：

3#工况(CC3)：在跨中处施加初始振幅(V0B30#=0.01 m，“0”下标表示初始状态，下同)，分别改变χc3、χc7值使得Ωc3=且Ωc7=。

通过比较图8(a)与图8(b)、图8(c)，发现在C3#和C7#分别与V5 和V3 阶整体模态频率满足“1∶1”条件后，两索各自产生了“拍”特性明显的内共振，各索的最大振幅约初始状态的5 倍。由图8(d)可得，当系统中存在两拉索与不同阶整体模态耦合引发多重内共振时，两索同振下的振幅和“拍”频周期与单索单振时基本一致。这表明在多根拉索与不同阶的竖向模态耦合产生“1∶1”内共振时，局部-整体间的能量交换仅发生于共振索与结构对应整体模态之间。为了验证这个推测，引入参数ξci表示Ci#的振幅最大值，选取8 索锚固点处的整体模态振型振幅()皆不为零的V7 阶整体模态作为研究对象，V7 阶整体模态下各拉索锚固点处振型振幅如图9 所示。

图8 CC3 工况条件下，C3#和C7#的振动响应图Fig.8 The vibration response of C3# and C7# under CC3

图9 V7 阶有索区梁段位置与其对应的Fig.9 The anchored position and its corresponding of the V7-order global mode

保留原CC3 基础模型、参数取值、运行设置不变，设置4#工况：

4-1#工况(CC4-1)：依次改变χc1～χc8使得各拉索将分别与V7 阶模态耦合产生“1∶1”内共振。此时系统中仍保留所有拉索参与系统内能量交换。

4-2#工况(CC4-2)：在CC4-1 基础上，将其他拉索简化为竖向弹性支承[18]，确保Ci#发生内共振时，动力系统中仅余留Ci#拉索且结构整体模态的振型及频率未发生变化。

汇总两子工况下的ξci如图10 所示。

图10 在CC4-1 和CC4-2 中，各拉索的ξci 变化折线图Fig.10 The variation trend of ξci under CC4-1 and CC4-2

由图10 可得，在两个子工况条件下，各拉索皆产生了剧烈的内共振。其中，ξci的最大差值发生在C4#处，但仅为0.00047 m。此外， C4#在CC4-1 和CC4-2 下的时程曲线变化规律基本一致，表明当多索同时与不同阶整体模态耦合产生内共振时，满足条件且共振的拉索仅与其对应阶次的结构整体模态发生能量转换作用，未满足共振条件的拉索不参与内共振系统能量转换。

4.3 与同阶整体模态耦合时的索-梁-索耦合效应

为研究与同一阶整体模态耦合时的索-梁-索耦合效应，基于CC3 工况设置5#工况条件如下：

5#工况(CC5)：在跨中处施加初始振幅(V0B30#=0.01 m)，分别改变χc2、χc5值使得Ωc2=Ωc5=。汇总C2#和C5#振动响应如图11 所示。

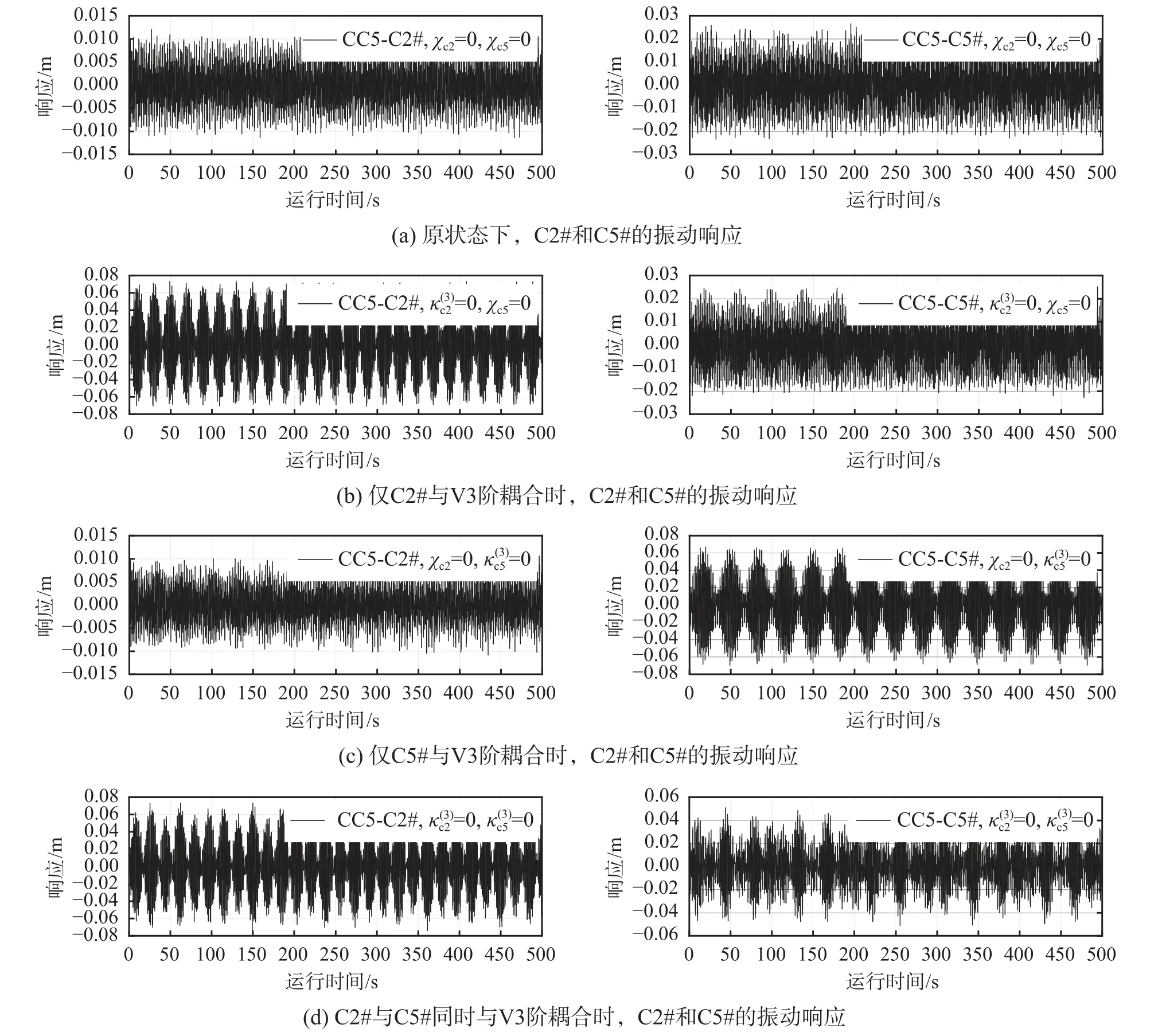
图11 CC5 工况条件下，C2#与C5#的振动响应图Fig.11 The vibration response of C2# and C5# under CC5

对比图11(a)、图11(b)、图11(c)和图11(d)，发现在C2#和C5#同时与V3 阶整体模态频率满足“1∶1”条件时，两索产生了“拍”特性明显的内共振，其最大振幅约是激励前的6 倍。与4.2 节中研究结果不同的是，当两索与同一阶整体模态耦合并产生多重内共振后，其共振特性发生了两点显著变化：① 激励后的拉索最大振幅变小；② “拍”的周期及振幅等特性发生变化。结合4.2 节研究成果，可以解释文献[27]中的研究现象，该研究中双斜拉索同时与代表了主梁的质量块第1 阶整体模态耦合产生多重内共振，所以一根拉索的振动会通过桥面影响到另一根拉索的振动特性。为进一步研究多索与同阶竖向模态耦合时的索-梁-索耦合效应，引入表示Ci#拉索在第k阶竖向振型激励作用下受到的多索效应被激励程度，由式(39)定义：

6#工况(CC6)：通过改变χci，使各个拉索分别与V3、V5、V7 阶整体模态耦合发生“1∶1”内共振。需要说明的是，由于C1#连接的B12#在第5 阶竖向振型下该梁段振幅值为所以略微调整拉索加入共振的顺序。汇总如图12所示。

图12 CC6 工况下，多索同振时的变化曲线Fig.12 The variation trend of under CC6 while multi-cables are vibrating

图12 可得，与V7 阶整体模态耦合产生的索-梁-索耦合效应主要体现为激励作用，而V3 和V5的耦合效应主要体现为抑制作用。工程中斜拉桥大多为密索体系设计，相邻拉索参数变化不大而导致其局部模态频率数值上非常接近，容易出现多索同时与某一阶整体模态耦合产生多重“1∶1”内共振现象，由于索-梁-索耦合效应有可能表现为是激励作用，激励产生的共振幅值或将达到单索结构下的2 倍。显然，这样条件下的设计是偏不安全的。然而，斜拉桥实际内共振行为非常丰富，索-梁-索耦合效应具体为激励或抑制作用，需与对应结构整体模态进行数值分析后判定。

4.4 多索同振的激励与被激励效应影响性分析

为精细分析两索与同阶整体模态耦合时的激励与被激励作用，同样选定频率数值较大的V7 阶整体模态在此作为研究对象。图9 中， V7 阶整体模态下各拉索锚固点处振型振幅满足关系式：

通过不重复地两两组合Ci#拉索与Cq#(q≠i)拉索并分别改变χci和χcq，使得Ωci≈Ωcq≈。此时，曲线说明了共振时Ci#被其他拉索激励效应程度，展示了Ci#的被激励效应；而曲线则说明了共振时Ci#激励其他拉索的激励效应程度，展示了Ci#的激励效应。此外，考虑到系统内共振中拉索的共振强度与其总质量(Mci)息息相关[29]，改变C2#、C6#拉索单位长度质量使得C2#、C3#和C6#总质量一致。基于此变化设置了 7#工况。

7-1#子工况(CC7-1)：在C1#、C3#、C6#、C8#的MA相同的情况下，变化χc1、χc3、χc6、χc8，使得此4 索分别与另外7 索同时与V7 阶整体模态耦合产生的索-梁-索耦合效应。此时，i∈{1, 3, 6, 8}，q∈[1, 8]。汇总如图13 所示。

图13 CC7-1 工况下， 变化曲线Fig.13 The variation trend of and under CC7-1

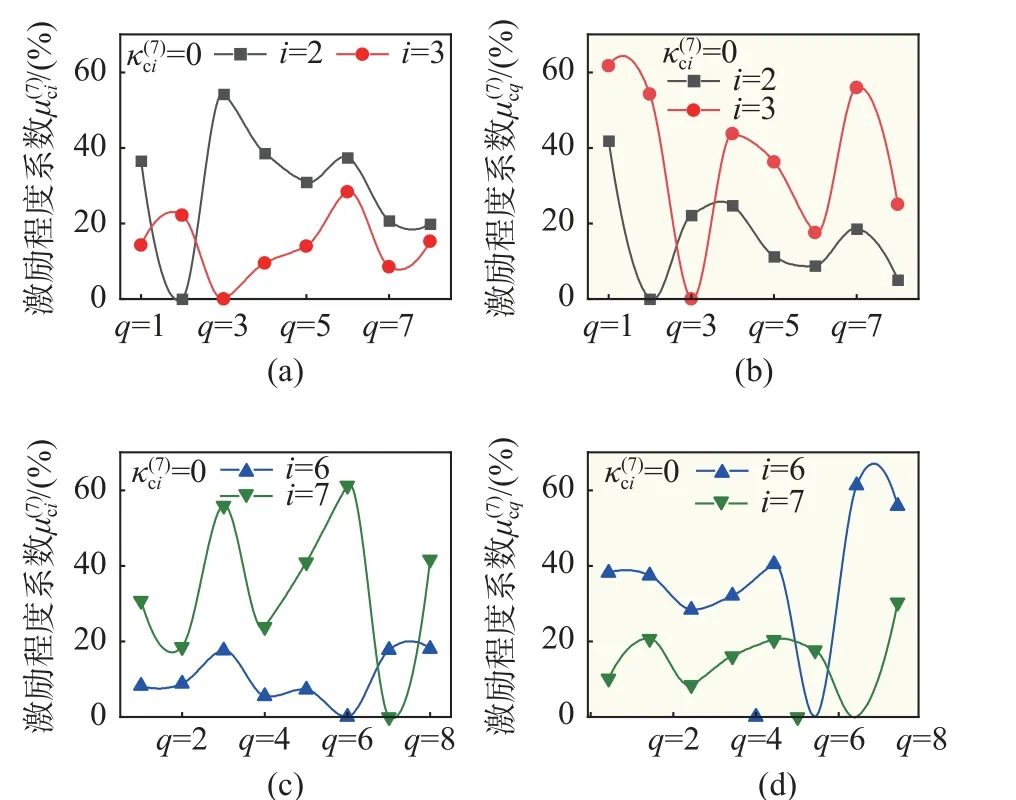
图14 CC7-2 工况下，的变化曲线Fig.14 The variation trend of and μ under CC7-2

5 结论

针对斜拉桥发生多重“1∶1”内共振时索-索间耦合效应将通过主梁传递而改变结构动力特性的问题，本文考虑索-梁几何非线性，建立了新的8 斜拉索-变截面梁的动力学模型，运用有限差分法及Galerkin 方法得到了斜拉桥动力方程组，分析了在多重内共振影响下的索-梁-索耦合效应，得到以下结论：

(1)通过对比有限元方法结果，验证了本文建立的动力学模型及其特征值解法能较为准确计算结构固有振动模态参数，针对运动方程的数值仿真结果观察到某根拉索局部模态频率与竖向某一阶整体模态频率比值满足“1∶1”时引发的“拍”的内共振现象，验证了本文模型的非线性动力特性。

(2)当多索与不同阶次整体竖向模态耦合而产生的多重“1∶1”内共振时，发生共振的拉索振动彼此相互独立，内共振下的系统能量交换仅发生于共振拉索与其对应阶次的整体模态之间。

(3)当多索与同一阶竖向整体模态耦合产生多重内共振时，索-梁-索耦合效应将改变结构的振动特性。本文8 索-梁耦合结构中，面内竖向第3 阶与第5 阶整体模态下的索-梁-索耦合效应为抑制作用，而第7 阶为激励作用。当多索同时面内竖向第7 阶整体模态耦合时，考虑了索-梁-索耦合效应的拉索最大幅值接近仅考虑单索内共振时的2 倍。

(4)相邻间距越小的索-梁-索耦合效应越显著，其激励效应与拉索质量、振型对应幅值呈正相关，而被激励效应与此两者呈反相关。

(5)本文建立的斜拉桥整体动力学模型更贴近工程实际结构，基于数值仿真的研究结果首次揭示了多重内共振下的索-梁-索耦合效应机理。下一步的研究将在斜拉桥整体结构的动力学精细化建模、拉索高阶非线性共振分析等方面进行。

此 外， Γci,1、 Γci,2、 Γci,3、 Γci,4、 Γci,5、 Γci,6、 Γci,7、Γci,8、 Γci,9、 Γci,10与 Γbj,1、 Γbj,2、 Γbj,3、 Γbj,4、 Γbj,5则分别 表示为相同形式下的8 阶和59 阶对角矩阵。为避免赘述，仅取 Γc,1和 Γb,1如下所示：

矩阵的各主元系数形式如下所示：

式(30)中，A和D是一个59×59 的矩阵，与主梁边界条件相关。本文中主梁左右侧边界为简支，在此条件下，为简化表达，定义Pp和Pp,q表达式为：

剪力影响矩阵A形式为：

轴力影响矩阵D形式如下所示：

式(A25)中，γi=Hcicosθci。