妙用三角形基本性质 巧解竞赛试题

☉

我们都知道三角形最基本的性质就是两边之和大于第三边，即：

性质1：在△ABC中，则a+b＞c，b+c＞a，c+a＞b.

反过来，我们也可以得到：

性质2：若正数a、b、c满足：a+b＞c，b+c＞a，c+a＞b，则a、b、c可作为三角形三边.

上述两个人尽皆知的性质（注：与其说性质，不如说是事实！）看似平凡，倘若灵活运用，其功能不俗.本文通过具体例子来展示上述两个性质的应用.

例1（1968年IMO试题）求证：在四面体ABCD中必存在某个顶点，使得从它发出的三条棱作为三边可以构成三角形.

证明：我们选一条最长的棱设为AB（若最长的棱有多条，则任选一条），如果从A，B各发出的三条棱可以构成三角形，则问题就解决了，若不然，则有：

AC+AD≤AB，BC+BD≤BA

⇒（AC+AD）+（BC+BD）≤2AB

⇔（AC+BC）+（AD+BD）≤2AB.

这显然是不可能的，因为在△ABC及△ABD中，依据性质1可得：

AC+BC＞AB，AD+BD＞AB

⇒（AC+BC）+（AD+BD）＞2AB.

评注：此题正是2011年清华大学自主招生试题.

例2 （2012年山东省竞赛试题）设A、B、C为圆x2+y2=1上不同的三点，若存在正数λ、μ，使得O—→C=λO—→A+μO—→B，则λ2+（μ-3）2的取值范围是_________.

解答：由于A、B、C为圆x2+y2=1上不同的三点，则：

平面直角坐标系λOμ中，作出λ、μ满足上述线性约束条件的可行域，而λ2+（μ-3）2则表示定点（0，3）到上述可行域内的动点距离平方，显然没有最大值，只有最小值，即为定点（0，3）到定直线λ-μ+1=0的距离的平方，即为2，故λ2+（μ-3）2的取值范围（2，+∞）.

评注：上述美妙的构思（例1本质就是反证法；例2本质就是向量加法的三角形法则）同时借助性质1获得让人难以置信的简证.有趣的是：例1也是2011年清华大学自主招生试题.

例3 （1998年伊朗数学奥林匹克试题）若c＞b＞a＞1，且a2-b2-c2+bc+b+c-1=0.

试判断a+b与c的大小关系.

解答：将已知条件适当变形得到：

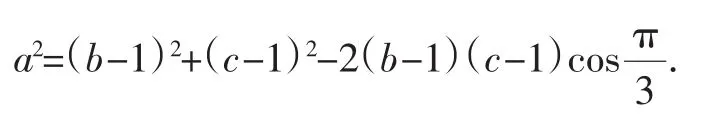
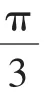
a+（b-1）＞c-1⇒a+b＞c.

例4 （2004年英国数学奥林匹克试题）若a、b、c均为正数，求证：

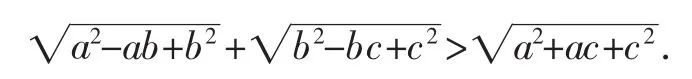
证明：适当变形，原不等式等价于：

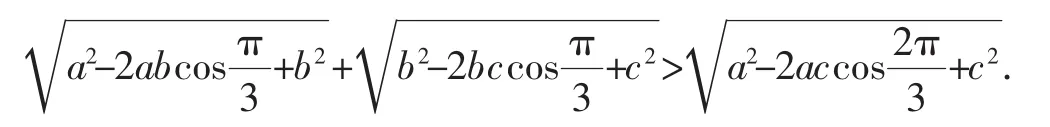
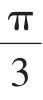
评注：例3、例4经过适当变形后，外部结构具有余弦定理的特征，构造三角形，借助性质1迅速获解，让人心旷神怡.

例5 （1989年全苏奥赛试题）设x，y，z＞0，xyz（x+y+z）=1，求（x+y）（y+z）最小值.

解答：设a=x+y，b=y+z，c=z+x，显然a+b＞c，b+c＞a，c+a＞b.

由性质2可得a、b、c构成三角形的三边，依据海伦公式（其中p为半周长）可得：

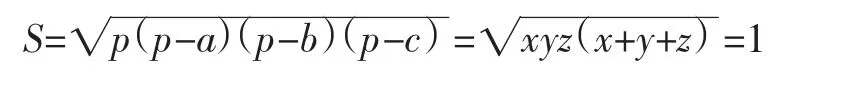
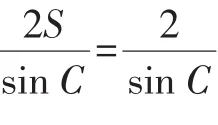
评注：简洁美就是数学美.数学往往是利用最基础、最简单的性质解决了极其复杂的问题，正所谓“四两拨千斤”.

例6 （2007年IMO试题）若x、y、z≥0，求证：

（x+y+z）（2xy+yz+zx）2≤3（y2+yz+z2）（z2+zx+x2）（x2+xy+y2）.

证明：（1）当x=0或y=0或z=0时，上述不等式显然成立；

（2）当x、y、z＞0时，设a=x+y，b=y+z，c=z+x，由性质2可得a、b、c构成三角形的三边，则p-a=z，p-b=x，p-c=y，故原不等式等价于：

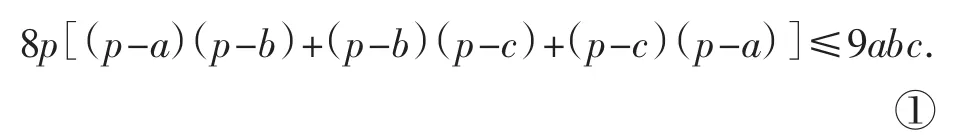
事实上，我们熟知△ABC中二个结论：

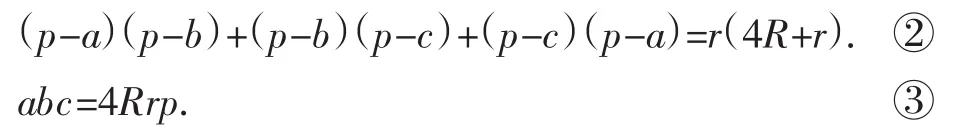
将上述②、③代入①，即只要证明R≥2r，这正是著名的欧拉定理.

评注：例6的确非常困难，几乎无从入手.初看例6，似乎与三角形毫无关系，但是通过换元：a=x+y，b=y+z，c=z+x就发现隐含“两个正数之和大于第三个正数”这一最简单的性质，这样为利用性质2奠定基础.构思奇特，让人拍案叫绝！

例7 （优美不等式）设a、b、c均为正数，且a+b+c=3，

证明：由已知条件可得所证不等式等价于：

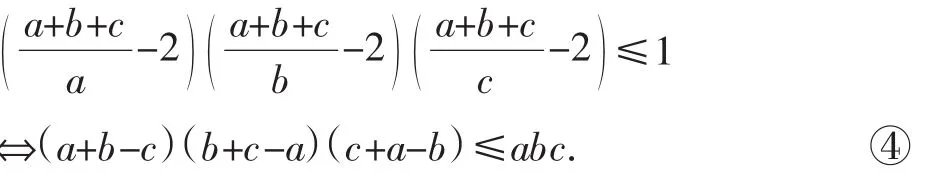
值得注意的是：式④是三角形中一个重要的不等式！

分析如下：显然因式a+b-c、b+c-a、c+a-b中最多一个非正数（否则矛盾！）.

（1）若上述三个因式中只有一个因式为非正数时，则不等式左边为非正数，而右边恒为正数，显然成立；

（2）若上述三个因式中没有非正数，即三个因式全为正数，此时：

a+b-c＞0、b+c-a＞0、c+a-b＞0

⇒a+b＞c，b+c＞a，c+a＞b.

由性质2可得a、b、c作为三角形三边，令a=x+y，b=y+z，c=z+x，则有：

（2x）（2y）（2z）≤（x+y）（y+z）（z+x）.

这是显然的，由二元均值不等式可得：

上述三式相乘即可得证.

评注：例7是文［1］中提出的26个优美不等式中的第19个不等式，有趣的是：例7就是依据2001年IMO试题改编而来，原题为：设a、b、c为正数，abc=1，求证：

（x+y-z）（y+z-x）（z+x-y）≤xyz.

这正是式④.

事实上，上述所举例题的确难度较大，乍看似乎无从入手.表面上看，这些试题好像与三角形没有必然的关系，甚至毫不相干，但是经过适当变形，尤其是精妙的构造后得到“任意两个正数之和大于第三个正数”，借助性质2，即构造三角形，再利用性质1来解决问题.

正如荷兰著名的数学家、数学教育家弗赖登塔尔所言，数学教师的首要任务就是引导和帮助学生进行再创造的工作，学生只有通过自己的再创造而获得的知识，才能被掌握并灵活运用.在新课改背景下，教师应当引导学生创造性地开发、拓展这些看似简单甚至不屑一顾但却蕴含巨大能量与价值的性质、结论，显得特别重要而紧迫，尤其对那些即将参加自主招生、各级各类竞赛的考生来说如虎添翼，这正是笔者本文的目的.

1.安振平.二十六个优美不等式［J］.中学数学教学参考（上旬），2010（1-2）.

5.王淼生.浅谈构造三角形的方法与策略［J］.课程教育研究，2012（7）.

6.王淼生.例谈一类换元法证明三角形不等式［J］.高中数理化（教师刊），2012（11）.