谈构造方程解三角函数问题

☉

有些题表面似乎难解，但当构造出方程后，不仅会迎刃而解，还会因构造的奇妙而拍手叫绝，妙趣横生.本文就对构造方程解三角函数问题进行归纳，供大家参考.

一、构造一元二次方程

例1求sin 18°的准确值.

分析：由于18°不是一个特殊值，不易求得，若注意到18°的5倍是90°，构造方程则易于解决问题.

解：设x=18°，有2x=90°-3x，sin 2x=cos 3x，2sinxcosx=4cos3x-3cosx.

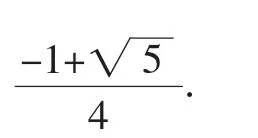
例2 锐角A、B、C满足：cos2A+cos2B+cos2C+2cosA·cosBcosC=1，求证：A+B+C=π.

分析：要找到三角之间的关系，必须把cosA、cosB、cosC中的一个用另外两个的代数式表示出来，为此只需按照构造主元法把已知条件整理成一个一元二次方程，便可解决问题.

解：构造方程x2+2cosBcosCx+cos2B+cos2C-1=0，则已知条件说明cosA是该方程的一个正根，即

为在［0，π］上y=cosx是单调函数，所以A=π-（B+C），即A+B+C=π.

二、构造二元一次方程

例3 若acos θ+bsin θ=c，acos φ+bsin φ=c（θ≠2kπ+φ，k∈Z）.

分析：由求证的结论联想到表示同一直线的两个二元一次方程的系数之间的关系，因此可通过构造二元一次方程设法解决.

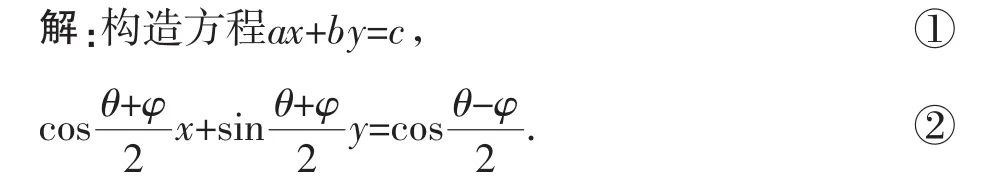
由已知条件，知P（cos θ，sin θ）、Q（cos φ，sin φ）满足方程①，即方程①表示直线PQ.

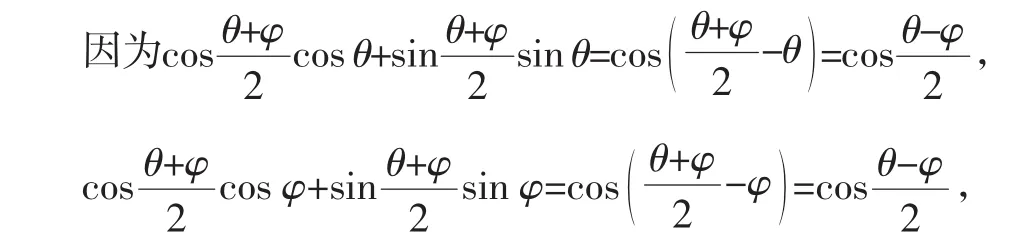
所以P（cos θ，sin θ）、Q（cos φ，sin φ）满足方程②，即方程②也表示直线PQ.

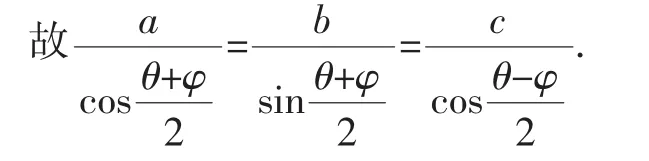
三、构造二元一次方程组

例4 已知sin α+sin β=b，cos α+cos β=a（a2+b2≤φ）.

求sin（α+β），cos（α+β）的值.

分析：本题的常规解法是联立已知条件组成方程组求出α与β的正、余弦值，再利用和角公式求出结果.但因为本题要求两个未知数，可设法构造二元一次方程组来解，培养学生的创造性思维，训练逆向思维.

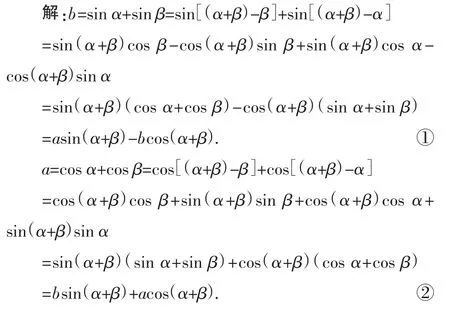
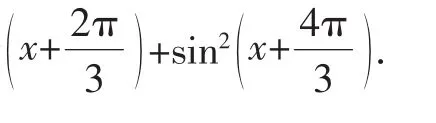
分析：由于sinx与cosx对偶，所以可尝试利用对偶式构造方程组求解.

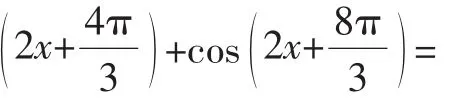
例6 若θ+φ=120°，试求cos2θ+cos2φ的最值.

分析：同上题.

解：令x=cos2θ+cos2φ，y=sin2θ+sin2φ，则x+y=2，x-y=cos 2θ+cos 2φ=-cos（θ-φ）.

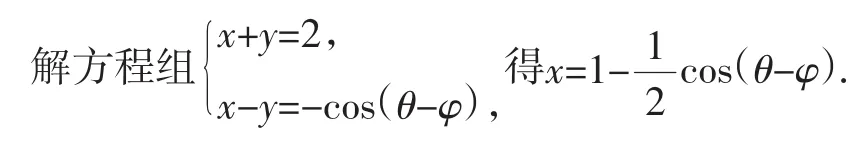
所以-1≤cos（θ-φ）=2-2x≤1.

四、构造二元二次方程

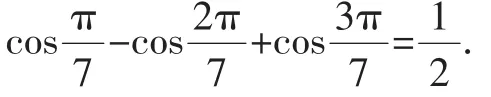
分析：由于sinx与cosx对偶，所以可尝试利用对偶式构造方程求解.

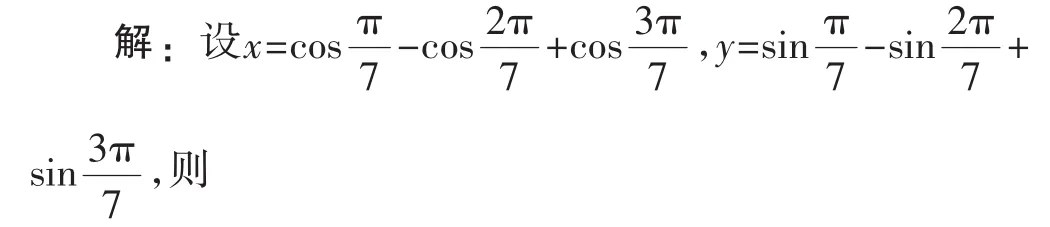
五、构造二元二次方程组

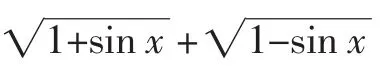
分析：由于题设条件中存在对偶关系，像1+sinx与1-sinx是对偶式，所以可利用对偶性构造方程组求解.

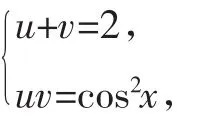
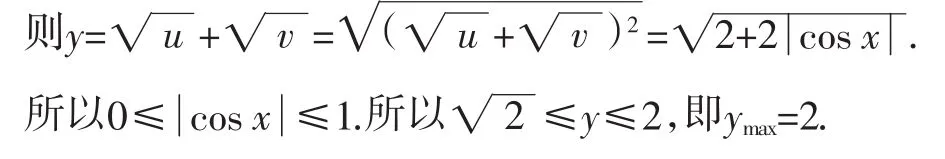
由①得v=y-u③，把③代入②得并整理得：

所以ymax=2.

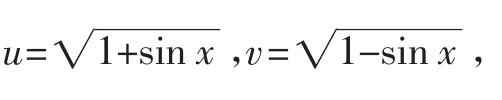
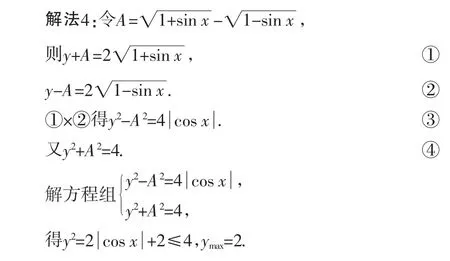
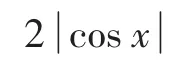
例9 求tan 22°30′准确值.

分析：由于22°30′不是一个特殊值，不易求得，若注意到22°30′的2倍是45°，构造方程则易于解决问题.

六、构造一元三次方程

例10 不同的三条直线xsin3α+ysin α=a，xsin3β+ysin β=a，xsin3γ+ysin γ=a（a≠0），有公共点，求证：sin α+sin β+sin γ=0.

分析：注意到三条直线方程的结构特征，可构造一个以sin α，sin β，sin γ为根的方程解决问题.

解：设不同三条直线方程的公共点为（h，k），则hsin3α+ksin α=a，hsin3β+ksin β=a，hsin3γ+ksin γ=a.

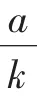
构造一元三次方程hx3+kx-a=0，由已知条件知sin α，sin β，sinγ是该方程的三个根，根据韦达定理得sinα+sinβ+sin γ=0.

七、构造三元一次方程组

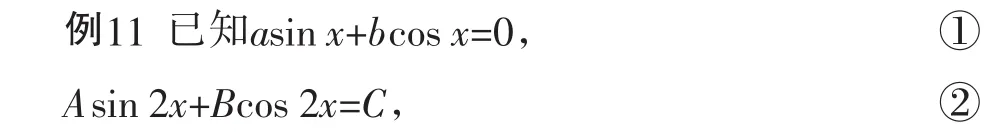
a，b不同时为0.

求证：2abA+（b2-a2）B+（a2+b2）C=0.

分析：观察已知条件①、②，应先根据倍角公式把两个方程的结构变成同一形式再设法构造方程组解决.

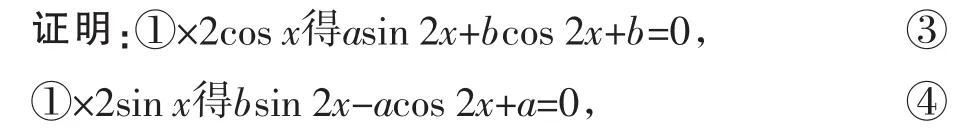
由此可见，构造方程解三角函数题不仅要有坚实广博的基础，还要有敏锐的观察力，由此及彼的联想能力及娴熟的转化技能.在平时的教学中，有目的地、有计划地向学生介绍这种解题思路，对提高纵横沟通知识的能力，发展创造性思维，提高解题能力都大有裨益.