比较得优劣 探究出新解

☉

第20届伊朗数学奥林匹克竞赛试题中的不等式证明题是一道形式简洁、内涵丰富的精彩赛题，引起了数学爱好者的广泛关注.笔者将从它的解法、变化和拓展加以研究，供读者参考.

题目：设a，b，c∈R+，a2+b2+c2+abc=4，证明：a+b+c≤3（第20届伊朗数学奥林匹克竞赛题）.

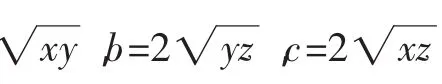
即xy+yz+xz+2xyz=1.

所以（xyz+xy+xz+x）+（xyz+xy+yz+y）+（xyz+xz+yz+z）

=3xyz+2xy+2yz+2xz+x+y+z

=xyz+xy+yz+xz+x+y+z+（xy+yz+xz+2xyz）

=xyz+xy+yz+xz+x+y+z+1，即

x（y+1）（z+1）+y（x+1）（z+1）+z（x+1）（y+1）

=（x+1）（y+1）（z+1），

由柯西不等式得，

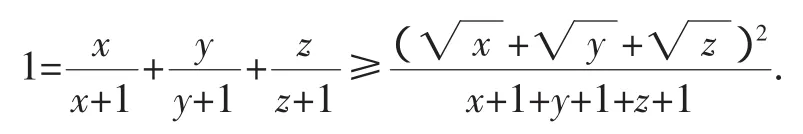
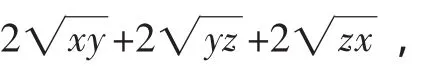
评注：这是文［1］给出的利用柯西不等式加以证明的方法，角度新颖，但需要有熟练的代数变形能力，技巧性较高.

证法2：由抽屉原理可知a，b，c中必有2个不大于1或者不小于1，不妨设为b，c，

由二元均值不等式得：

4-a2=b2+c2+abc≥2bc+abc=bc（2+a）.

由①②得，2-a≥b+c-1，故a+b+c≤3.

评注：这是文［2］给出的利用抽屉原理妙证不等式的方法，构思独特，堪称经典.

证法3：将a2+b2+c2+abc=4变形得：

4=（a+b+c）2-2（ab+bc+ca）+abc

=（a+b+c）2-（2-a）（2-b）（2-c）-4（a+b+c）+8

=［（a+b+c）-2］2-（2-a）（2-b）（2-c）+4，

即［（a+b+c）-2］2=（2-a）（2-b）（2-c）.

由题设知2-a，2-b，2-c都是正实数，利用三元均值不等式得：

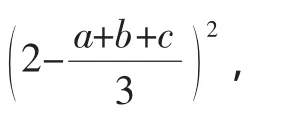
化简得：（a+b+c）［（a+b+c）-3］≤0，

所以a+b+c≤3.

评注：这是文［3］通过配方后利用三元均值不等式给出的证明，同样需要熟练的代数变形能力.

证法4：由a2+b2+c2+abc=4得，

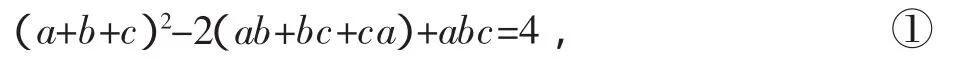
考虑（2-a）（2-b）（2-c）=8-4（a+b+c）+2（ab+bc+ca）-abc.

由题设条件可知2-a，2-b，2-c均为正.

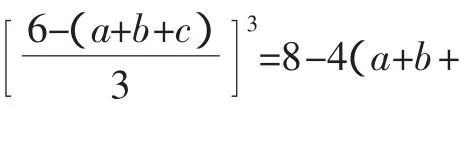
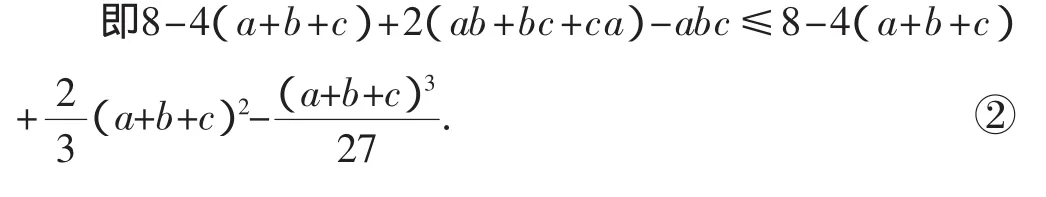
①+②并设a+b+c=t得t3+9t2-108≤0，即（t-3）（t+6）2≤0.

因为（t+6）2＞0，所以t≤3，所以原不等式成立.

评注：在文［4］中用构造因式证明三元不等式的方法给出的证明.它的要领是：

构造因式（m-x）（m-y）（m-z），利用均值不等式使x+y+z（或x2+y2+z2），xy+yz+zx，xyz三者关系有机结合起来，使问题得到突破.这一方法可规避技巧性较高的式子变形，使问题的解决具有可操作性，学生较容易掌握.但不足的是过程较复杂且实用性不强.

综观上述赛题的四种证明方法，总觉巧妙有余，简洁不够且自然不足.正如美籍匈牙利数学家波利亚所言：“聪明的学生和聪明的读者不会满足于只验证推理的各个步骤都是正确的，他们也想知道各个不同步骤的动机和目标”，“如果最为引人注目的步骤其动机和目的仍不可理解的话，那么他们在推理和创新方面学不到任何东西”.我们研究一个问题不仅希望得到一个解答，也希望这个解答是优美的、富有启发性的，更渴望知道这个解答是如何想到的，只有这样才能让学生信服和接受，才能有效地做好学生解题辅导（尤其是竞赛辅导）工作.因此揭示问题解决的心理过程和分析探索过程，引导学生寻找最简洁自然的解题方法，是提高学生的解题能力乃至培养提高他们的思维能力、探究能力和创新能力的有效途径.同时，现实施的新课程已降低了不等式证明的要求，照上述方法讲解，大部分学生仍难以理解.爱因斯坦说过“数学美，本质上终究是简单性”.鉴于此笔者经过探究，获得了这个优美赛题的两个简洁自然的证明.

证法5：已知条件变形得，a2+（bc）a+b2+c2-4=0，

利用一元二次方程求根公式得：

要证明原不等式只需证明：

而（b+c-2）2≥0是显然成立的，故原不等式得证.

评注：证法5中根据已知条件是二次特征，利用求根公式消元后，采用分析法简单地获得了原不等式的证明.这样的方法流畅自然，赏心悦目！正如克莱因所说“一个精彩巧妙的证明，精神上近乎一首诗”.

证法6：假设a+b+c＞3，则c＞3-a-b，故：

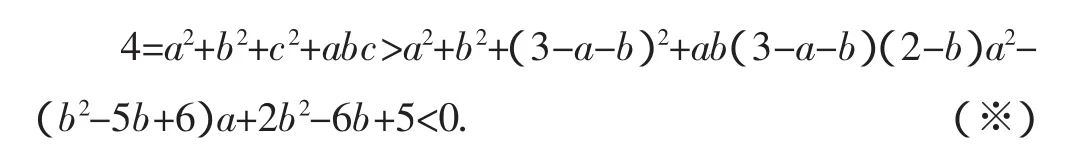
由条件知2-b＞0，

驻=（b2-5b+6）2-4（2-b）（2b2-6b+5）

=（2-b）［（2-b）（3-b）2-4（2b2-6b+5）］

=（2-b）（-b3+3b-2）=（2-b）（1-b）（b2+b-2）

=-（2-b）（1-b）2（b+2）.

在0＜b＜2的条件下驻≤0，故（※）式恒不成立，从而原不等式成立.

评注：证法6采用反证法，代入条件，考察抛物线开口与“△”情况，结合二次函数性质立即得出矛盾，相当简洁，同样给人美的享受.

对于一道数学题目，当寻觅到一种妙解、巧证，宛如一弯绚丽的彩虹，折射出智者的光辉、体现出数学之魅力，这正是数学简洁之美！至此，问题似乎得到了完美解决，然而波利亚有精辟的名言：“没有一道题是解决得十全十美的，总剩下一些工作要做，经过充分的探讨、总结总会有点滴的发现，而且在任何情况我们总能提高对解答的理解水平.”因此，我们再来探究本题的一些变化和拓展.

问题1：（《数学通讯》（上）2012年第3期数学问题征解86）

已知a，b，c∈R+且满足a2+b2+c2+abc=4，证明：4a+4b+3c≤ab+10.

分析：本题是原竞赛题改编而来，采用前四种方法均可给出本题的证明，但若采用后两种方法就难以入手.

证明：由抽屉原理知在a、b、c三个正实数中必有两数同时不大于1或不小于1，不妨设为a，b，则（a-1）（b-1）≥0，ab-（a+b）+1≥0，即a+b-1≤ab.①

由条件得4-c2=a2+b2+abc≥2ab+abc=ab（2+c），

所以2-c≥ab≥a+b-1，所以a+b+c≤3. ②

由①+3×②得4a+4b+3c≤ab+10，等号当且仅当a=b=c=1时取到.

说明：本题虽利用前四种方法均可加以证明，但用构造抽屉原理证明最简洁.

问题2：设a，b，c≥1，且满足abc+2a2+2b2+2c2+ac-bc+4a+4b-c=28，求a+b+c的最大值.（2011年全国数学联赛加试B卷第三题）

分析：已知条件可化为2（a-1）2+2（b+1）2+2c2+（a-1）（b+1）c=32，

令x=a-1，y=b+1，z=c，则问题转化为：已知2x2+2y2+2z2+xyz=32，求x+y+z的最大值.此即为原竞赛题形式，因此，这个联赛题的本质与原竞赛题是一样的，采用上述几种方法均可加以处理，有兴趣的读者可自行尝试完成.

问题3：（《数学通讯》（上）2013年第3期问题征解128）

设实数a，b，c满足a2+b2+c2+abc=4，且-2＜a≤2.试证：a+b+c≤3.

说明：本题对原赛题的正实数a，b，c条件放宽到实数a，b，c，-2＜a≤2，是对原赛题的一个拓展.实际上，条件还可进一步放宽即得问题4.

问题4：若实数a，b，c满足a2+b2+c2+abc≤4，则a+b+c≤3.

证明：将已知条件变形得，a2+（bc）a+b2+c2-4≤0，所以

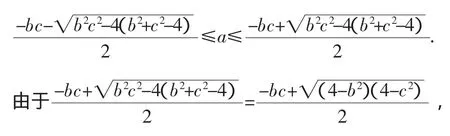
故要证明原不等式只需证明

最后一个不等式是显然成立的，故原不等式得证.

问题5：已知a，b，c为正实数，满足a3+b3+c3+abc=4，求证：a+b+c≤3.

说明：这是文［5］得出的一个与赛题类似的不等式，是对原赛题的延拓.事实上，条件可放宽，从而得到问题6.

问题6：已知a，b，c为正实数，满足a3+b3+c3+abc≤4，求证：a+b+c≤3.

证明：由抽屉原则可知，在正实数a，b，c中必有2个同时不小于1，或者不大于1，不妨设为b，c，于是有

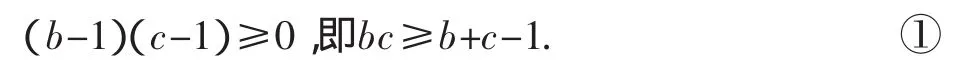
由三元均值不等式得：

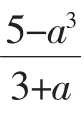
⇔（a-1）（2a+1）≥0，这是成立的，所以有a+b+c≤3.

这些解法让我们深深体会到一些美丽的数学结论往往形式简单，但证明却隐藏得极深.由此可见，数学是人类思考中的最高成就，是各式各样的证明技巧，是研究抽象结构的理论，是一种理性的精神，使人类的思维得以运用到最完善的程度.而对数学方法的研究，常常比解决数学问题本身更重要.

1.陈继雄.一道赛题的另一种证法［J］.中学数学教学参考，2011（1-2）.

2.安振平.妙用抽屉原理证明不等式［J］.数学通报，2011（1）.

3.范花妹，等.探究一道伊朗数学竞赛题［J］.数学通讯（上），2011（11-12）.

4.查正开.构造因式处理一类三元问题［J］.中学数学月刊，2012（2）.

5.沈毅.一道伊朗竞赛题的探究［J］.中等数学，2012（7）：11.