关于单位圆内亚纯系数线性微分方程解的微分多项式的值分布

占美龙，郑秀敏

(江西师范大学数学与信息科学学院，江西南昌330022)

0 引言和主要结果

继J.Heittokangas系统研究单位圆Δ内线性微分方程之后，许多国内外学者在这方面作了进一步研究，并取得了若干重要成果［1-6］.对于复平面C上的线性微分方程，前人得到了许多关于方程解的微分多项式的重要估计［7-8］.然而，由于Δ与C本质上有很大不同，所以研究Δ内线性微分方程解的微分多项式具有重要意义.近年来，曹廷彬和仪洪勋在文献［3］中对Δ内的2阶线性微分方程进行研究，得到了方程解的零点收敛指数的估计.之后，A.El Farissi等对其结果进行推广，得到了Δ内线性微分方程解的微分多项式的零点分布.特别地，A.El Farissi等在文献［4］中对2阶非齐次线性微分方程

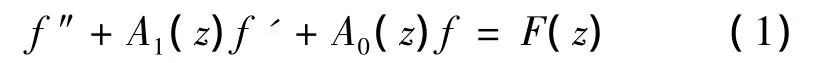
进行了研究，得到了当方程系数为Δ内解析函数时，方程(1)的解的微分多项式取小函数值点的迭代收敛指数的估计.在叙述其结果之前，为方便起见，定义

其中A0(z)(≢0)，A1(z)，d0(z)，d1(z)，d2(z)(d0(z)，d1(z)，d2(z)不全为零)，φ(z)(≢ 0)，F(z)(≢ 0)是Δ内的解析函数.

定理A［4］设A0(z)(≢0)，A1(z)和F(z)(≢0)是Δ内有穷级解析函数，d0(z)，d1(z)，d2(z)是Δ内不全为零的有穷级解析函数且满足h(z)≢0(其中h(z)由(4)式给出).又设φ(z)(≢0)是Δ内有穷级解析函数，且使得ψ(z)不是方程(1)的解(其中ψ(z)由(5)式给出).若f(z)是方程(1)的无穷级解且满足σ2(f)=σ，则微分多项式

满足

和

文献［5］对2阶齐次线性微分方程

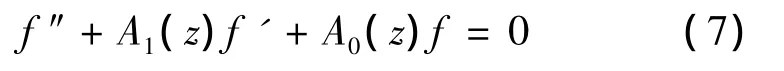
进行了研究，得到结果如下.

定理B 设A0(z)，A1(z)是Δ内解析函数且满足i(A0)=p，σp(A1)＜σp(A0)=σ(0＜σ＜∞)，或者 σp(A1)=σp(A0)=σ(0＜σ＜∞)且τp(A1)＜τp(A0)= τ(0＜ τ＜∞).又设 d0(z)，d1(z)是Δ内不全为零的解析函数且满足max{σp(d0)，σp(d1)}＜ σp(A0)，φ(z)(≢0)是 Δ内解析函数且满足σp(φ)＜∞.若f(z)(≢0)是方程(7)的解，则微分多项式

满足

和

其中

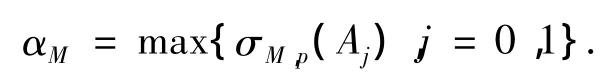
在定理A和定理B中，方程(1)和(7)的系数以及微分多项式(6)和(8)的系数均为Δ内解析函数.自然就提出如下问题:当方程(1)和(7)的系数以及微分多项式(6)和(8)的系数均为Δ内亚纯系数时，能否得到类似的结论?本文对该问题进行研究，并进一步讨论迭代下级的情况，得到了以下结果.

定理1 设A0(z)(≢ 0)，A1(z)，d0(z)，d1(z)，d2(z)(d0(z)，d1(z)，d2(z)不全为零)和 F(z)(≢0)为 Δ内亚纯函数且满足max{i(A0)，i(A1)，i(dj)，j=0，1，2，i(F)}=p，同时使得h(z)≢0(其中h(z)由(2)～(4)式给出).又设φ(z)(≢0)是Δ内亚纯函数且满足σp(φ)＜∞，同时使得ψ(z)不是方程(1)的解(其中ψ(z)由(2)～(5)式给出).若f(z)是方程(1)的无穷p次迭代下级亚纯解且满足μp+1(f)=μ，则微分多项式(6)满足φ)=μp(gf)= μp(f)= σp(f)= σp(gf)=φ)=∞和.又若f(z)是方程(1)的有穷p次迭代下级亚纯解且满足max{σp(A0)，σp(A1)，σp(dj)，j=0，1，2，σp(F)，σp(φ)}＜μp(f)，则微分多项式(6)满足

定理2 设A0(z)(≢ 0)，A1(z)，d0(z)，d1(z)，d2(z)(d0(z)，d1(z)，d2(z)不全为零)是Δ内亚纯函 数， 且 满 足max{σp(A1)，λp(1/A0)，λp(A0)，σp(dj)，j=0，1，2}＜ μp(A0)≤σp(A0)＜∞.又设φ(z)(≢0)是Δ内亚纯函数且满足σp(φ)＜∞，同时使得α1φ'≢β1φ(其中α1，β1分别由(2)和(3)式给出).若f(z)(≢0)是方程(7)的亚纯解，则微分多项式(6)满足

和

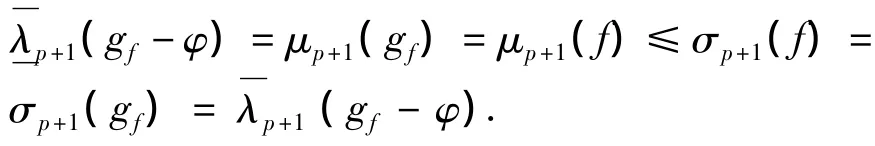
进一步，考虑高阶齐次线性微分方程

和微分多项式

其中A0(z)(≢0)，…，An-1(z)，d0(z)，…，dn(z)(d0(z)，…，dn(z)不全为零)是Δ内亚纯函数.用类似定理2 的证明方法可得到类似结果，故此处略去证明.在叙述结果之前，为方便起见，定义

其中 Cj(z)，j=0，…，n-1 是 Δ 内仅依赖于 αi，j(i，j=0，…，n-1)的亚纯函数，φ(z)(≢0)是Δ内亚纯函数.

定理 3 设A0(z)(≢ 0)，A1(z)，…，An-1(z)，d0(z)，…，dn(z)(d0(z)，…，dn(z)不全为零且满足max{i(d0)，…，i(dn)}=p)是Δ内亚纯函数，且满足max{σp(A1)，…，σp(An-1)，λp(1/A0)}＜ μp(A0)≤σp(A0)＜∞，同时使得h1(z)≢0(其中h1(z)由(11)～(13)式给出).又设φ(z)(≢0)是Δ内亚纯函数且满足σp(φ)＜∞，同时使得ψ1(z)≢0(其中ψ1(z)由(14)式给出).若f(z)(≢0)是方程(9)的亚纯解，则微分多项式(10)满足

和

1 定义和记号

定义1 Δ内亚纯函数f(z)的p次迭代级定义为

定义2［11］Δ内亚纯函数f(z)的p次迭代下级定义为

定义3 Δ内亚纯函数f(z)的级的增长指标定义为

定义4 Δ内亚纯函数f(z)的a-值点序列(a∈C∪{∞})的迭代收敛指数定义为

f(z)的不同a-值点序列(a∈C∪{∞})的迭代收敛指数定义为

定义5［11］Δ内亚纯函数f(z)的a-值点序列(a∈C∪{∞})的迭代下收敛指数定义为

f(z)的不同a-值点序列(a∈C∪{∞})的迭代下收敛指数定义为

(ii)进一步地，在定义4和定义5中用小函数φ(z)代替a，可得和的定义.

2 定理证明所需引理

引理1［8］设f(z)是Δ内亚纯函数且k∈N，则有m(r，f(k)f)=O(log+T(r，f)+log(1-r)-1)，至多除去1个例外集E⊂［0，1)且满足∫Edr/(1-r)＜∞.若f(z)是有穷级，则有

引理2［12］设g(r)和h(r)是［0，1)上单调递增函数且满足g(r)≤h(r)，至多除去1个例外集E⊂［0，1)且满足，则存在1个常数d∈(0，1)，使得 g(r)≤h(s(r))对所有的r∈［0，1)成立，其中s(r)=1-d(1-r).

引理3 设A0(z)，A1(z)，…，An-1(z)是Δ内亚纯函数且满足max{λp(1/A0)，σp(Aj)，j=1，…，n-1}＜μp(A0)＜∞.若f(z)是方程(9)的非零亚纯解，则有μp(f)=σp(f)=∞.

证设f(z)是方程(9)的非零亚纯解.将方程(9)改写成

由引理1可知

记σ1=max{λp(1/A0)，σp(Aj)，j=1，2，…，n-1}，μ= μp(A0)，则σ1＜ μ.∀ε(0＜ 2ε＜ μ -σ1)及r→1-有

由(15)～(18)式可得

由引理2和(19)式得μp(f)=σp(f)=∞.

引理3得证.

引理4 设f(z)是Δ内亚纯函数，则

(i)σp(f)= σp(1/f)，σp(a·f)= σp(f)(a∈C{0});

(ii)σp(f')= σp(f);

(iii)max{σp(f+g)，σp(fg)}≤max{σp(f)，σp(g)};

(iv)若 σp(f)＞ σp(g)，则

引理5［13］设f(z)是Δ内亚纯函数，则

(i)μp(f)= μp(1/f)，μp(a·f)= μp(f)(a ∈C{0});

(ii)μp(f')= μp(f);

(iii)max{μp(f+g)，μp(fg)}≤max{μp(f)，σp(g)}或max{σp(f)，μp(g)};

(iv)若 μp(f)＞ σp(g)，则

引理 6［14］设A0(z)，…，An-1(z)，F(z)(≢ 0)是Δ内亚纯函数.若f(z)是方程

的亚纯解，且满足max{σp(F)，σp(Aj)，j=0，1，…，n-1}＜ σp(f)≤∞，则

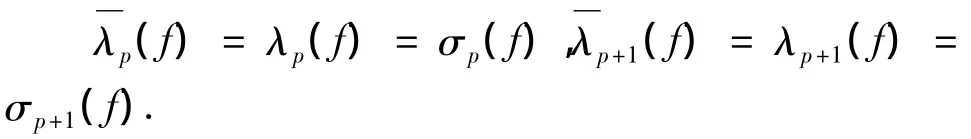
引理7 设A0(z)，…，An-1(z)，F(z)(≢0)是Δ内亚纯函数.若f(z)是方程(20)的亚纯解，且满足max{σp(F)，σp(Aj)，j=0，1，…，n-1}＜ μp(f)≤∞，则μp+1(f).

证用类似引理6的证明方法即可证得.

引理8 设f(z)是Δ内亚纯函数且满足max{λp(f)，λp(1/f)}＜ μp(f)，a(z)(≢ 0)，b(z)，c(z)，d(z)均为 f(z)的小函数，则微分多项式a(z)f2+b(z)f+c(z)f'+d(z)满足

证由max{λp(f)，λp(1/f)}＜ μp(f)可知当r→1-时，有

N(r，f)=o(T(r，f))，N(r，1/f)=o(T(r，f)).

又由引理1可知

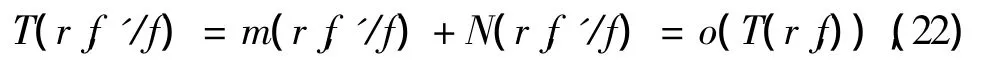
其中 r→1-，且 r∉ E，E ⊂［0，1)且满足∫Edr/(1-r)＜∞.

一方面，由(22)式可知

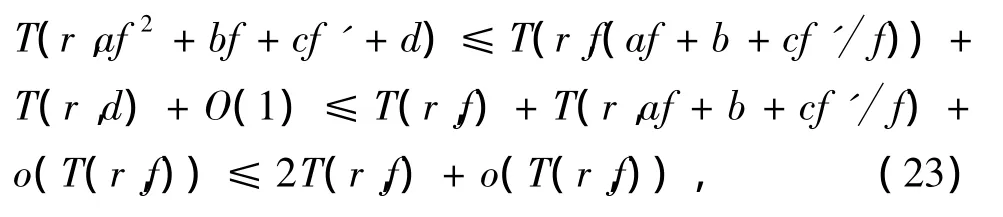
其中 r→ 1-，且 r∉ E1，E1⊂［0，1)且满足∫E1dr/(1-r)＜∞.再由引理2和(23)式可得

另一方面，由(22)式亦可知

其中 r→1-，且 r∉ E2，E2⊂［0，1)且满足(1-r)＜∞.再由引理2和(24)式可得

综上所述，σ(af2+bf+cf'+d)= σ(f)，即(21)式成立.

引理8得证.

3 定理的证明

定理1 的证明设f(z)是方程(1)的无穷p次迭代下级亚纯解且满足μp+1(f)=μ.将方程(1)改写成

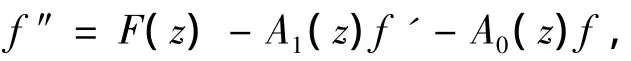
则由(6)式可得

由(25)式可得

其中α0，α1如(2)式所定义.对(26)式2边微分得gf'-(d2(z)F(z))'- α1F(z)= β1f'+ β0f，(27)其中β0，β1如(3)式所定义.考虑关于f和f'的方程组

因已知h(z)≢0，故解方程组(28)得

若μp(gf)＜∞，则由引理4和引理5及(29)式可得μp(f)＜∞，矛盾.故

一方面，由引理4和引理5及(6)式可得μp+1(gf)≤μp+1(f)，σp+1(gf)≤σp+1(f).另一方面，由引理 4和引理 5及(29)式可得 μp+1(f)≤μp+1(gf)，σp+1(f)≤σp+1(gf).故

μp+1(gf)=μp+1(f)≤σp+1(f)=σp+1(gf).

记ω=gf-φ.由于σp(φ)＜∞，因此有

和

将gf=ω+φ代入(29)式可得

其中ψ(z)如(5)式定义.将(30)式代入方程(1)得

其中 φi(z)(i=0，1，2)是 Δ内亚纯函数且满足σp(φi)＜∞(i=0，1，2).已知ψ(z)不是方程(1)的解，故 F(z)-(ψ″+A1(z)ψ'+A0(z)ψ)≢0.从而，由引理6可得λp+1(ω)= σp+1(ω)，由引理7可得，即λp(gfφ)=μp(gf)= μp(f)= σp(f)= σp(gf)=φ)=∞和σp+1(f)= σp+1(gf)

又若f(z)是方程(1)的有穷p次迭代下级亚纯解且满足

由(25)和(32)式及引理4和引理5可得μp(gf)≤μp(f)，σp(gf)≤σp(f).下证 μp(gf)=μp(f)，σp(gf)= σp(f). 若 μp(gf)＜ μp(f)，σp(gf)＜σp(f)，则由(29)和(32)式可得μp(f)≤max{σ1，μp(gf)}＜ μp(f)，σp(f)≤max{σ1，σp(gf)}＜σp(f)，矛盾.故μp(gf)= μp(f)≤σp(f)= σp(gf).

记 ω=gf- φ.因为 σp(φ)＜ μp(f)，所以

用上述同样方法易得方程(31)，其中 φi(z)(i=0，1，2)满足σp(φi)＜ μp(f)(i=0，1，2).故由引理6可得，由引理7可得，即

定理1 得证.

定理2 的证明 设f(z)是方程(7)的亚纯解，则由引理3可知μp(f)=σp(f)=∞.将方程(7)改写成

则由(6)式可得

其中α0，α1如(2)式所定义.对(33)式2边微分可得

其中β0，β1如(3)式所定义.考虑关于f和f'的方程组

其中

若d2(z)≢0，则由已知条件和引理8可知σp(h)=σp(A0)＞ 0，故h(z)≢0.若d2(z)≡0，d1(z)≢0，则由(35)式可知

进而由σp(h)=σp(A0)＞0可知h(z)≢0.若d2(z)≡0，d1(z)≡0，d0(z)≢0，则h(z)=-d20(z)≢0.综上所述，h(z)≢0.故解方程组(34)得

其中 σp(α1)＜∞，σp(β1)＜∞，σp(h)＜∞.若μp(gf)＜∞，则由引理4和引理5及(36)式可知μp(f)＜∞，矛盾.故 μp(gf)= μp(f)= σp(f)=σp(gf)=∞.

一方面，由引理4和引理5及(33)式可得μp+1(gf)≤μp+1(f)，σp+1(gf)≤σp+1(f).另一方面，由引理 4和引理 5及(36)式可得 μp+1(f)≤μp+1(gf)，σp+1(f)≤σp+1(gf).故 μp+1(gf)= μp+1(f)，σp+1(gf)= σp+1(f).

记ω=gf-φ.由于σp(φ)＜∞，因此有

和

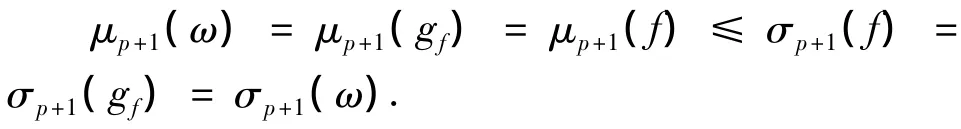
将gf=ω+φ代入(36)式可得

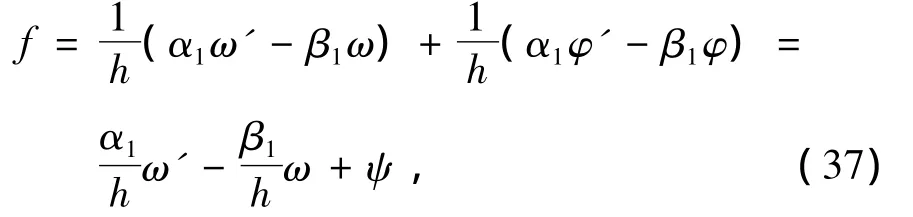
其中ψ(z)=(α1φ'- β1φ)/h≢0.将(37)式代入方程(1)可得

其中 φi(z)(i=0，1，2)是 Δ内亚纯函数且满足σp(φi)＜∞(i=0，1，2). 又由 σp(φ)＜∞可知σp(ψ)＜∞.从而，由引理3及ψ(z)≢0可知ψ(z)不可能是方程(1)的解，即

ψ″+A1(z)ψ'+A0(z)ψ ≢0.故由引理 6可得σp+1(ω)，由引理7可得，即

和

定理2 得证.

［1］ Cao Tingbin，Yi Hongxun.The growth of solutions of linear differential equations with coefficients of iterated order in the unit disc ［J］.J MathAnalAppl，2006，319(1):278-294.

［2］Cao Tingbin.The growth，oscillation and fixed points of solutions of complex linear differential equations in the unitdisc ［J］.JMathAnalAppl，2009，352(2):739-748.

［3］曹廷彬，仪洪勋.关于单位圆内解析系数的二阶线性微分方程的复振荡 ［J］. 数学年 刊，2007，28A(5):719-732.

［4］ FarissiA El，BelaïdiB，Latreuch Z.Growth and oscillation of differential polynomials in the unit disc［J］.Electron J Diff Equ，2010，87:1-7.

［5］ Belaïdi B.Growth and oscillation of some class of differential polynomials in the unit disc ［J］.Kragujevac J Math，2011，35(3):369-386.

［6］Heittokangas J.On complex differential equations in the unit disc［J］.AnnAcad Sci Fenn Math Diss，2000，122:1-54.

［7］ FarissiA El，Belaïdi B.On oscillation theorems for differential polynomials ［J］.Electron J Qual Theory Differ Equ，2009，22:1-10.

［8］LaineI，Rieppo J.Differential polynomials generated by linear differential equations ［J］.ComplexVar TheoryAppl，2004，49(12):897-911.

［9］ Hayman W K.Meromorphic functions ［M］.Oxford:Clarendon Press，1964.

［10］ LaineI.Nevanlinna theory and complex differential equations［M］.Berlin:Walter de Gruyter，1993.

［11］胡汇.复平面及单位圆内齐次线性微分方程解的增长性和值分布［D］.南昌:江西师范大学，2013:1-43.

［12］Bank S B.A general theorem concerning the growth of solutions of first-order algebraic differential equations［J］.Compositio Math，1972，25(1):61-70.

［13］涂金，黄海霞，徐洪焱，等.单位圆内亚纯函数与解析函数的级与型［J］.江西师范大学学报:自然科学版，2013，37(5):449-452.

［14］Cao Tingbin，Deng Zhongshu.Solutions of non-homogen eous linear differential equations in the unit disc ［J］.Ann Polon Math，2010，97(1):51-61.