An Update Logic for Games with Angry Players*

Fan Huang

Institute of Logic and Cognition，Sun Yat-sen University

wong.vanz@gmail.com

Xuefeng Wen

Institute of Logic and Cognition，Sun Yat-sen University

wxflogic@gmail.com

An Update Logic for Games with Angry Players*

Fan Huang

Institute of Logic and Cognition，Sun Yat-sen University

wong.vanz@gmail.com

Xuefeng Wen

Institute of Logic and Cognition，Sun Yat-sen University

wxflogic@gmail.com

.Angry players in games often make aggressive decisions to minimize their opponents'payoffs even if they are fully aware that their actions are going against their personal interest.We model such behaviour pattern with angry update operators in modal logic.Instead of modifying the angry player's preference for update，we restrict her strategic accessibility relation so that only those actions leading to her opponent's lowest payoff are kept.We construct an axiomatic system for the logic and prove its soundness and weak completeness.Finally，we apply the logic to ultimatum games in which the responder is angry.

1　Introduction

This paper focuses on the emotion of anger，and develops a modal logic to characterise the effect of anger on human behaviour in sequential games.Human emotion isnotoftenseenasapropersubjectforlogicalstudy（foranexception，see［1］），mainly because most emotions have complex cause and unstable consequence.This paper thereby focuses on the emotion of anger，which is one of the most sustainedly investigated emotions（for a review，see［2］）.Anger，unlike many other emotions such as envy or pride，has relatively stable behaviour pattern，especially in the context of games（［11］）.One famous example is the ultimatum game，where in response to unfair treatment，angry responders tent to reject proposals that they can certainly benefit from［7，8］.Such aggressive behaviour is often treated as the consequence of anger（［2］），which regardless of the angry players'own costs minimises their opponents' payoffs.We model this relatively stable consequence of anger in games using modal logic with update operators.

When a player is angry and intends to minimise her opponents'payoff，she will do that even when she is fully aware that such choice may well be going against her own interest.This property of anger in games requires two sets of accessibilityrelations between possible states in our model of modal logic，one for players'preferences，and the other for players'strategic choice.These two sets of relations allow us to employ an angry update of models，which restricts the angry player's strategic choice while keeping her preference.Particularly，an angry player's strategic choice is so restricted after an angry update that only those strategies that give her opponent the lowest payoff survive，which means that all states that give the opponent a higher payoff is not reachable by the angry player's strategic action.

Angry update changes players'choice in a different way from previous works of modal logic，in which players'preferences were overwritten（for an example，see［10］）.First，since most actions are not strategically available after angry updates，the space for the angry player to manipulate the outcome by adopting other kinds of rationality（e.g.，by maximising the payoff of a coalition）is extremely restricted. Second，angry updates keep all the players'preference relations，which means that the model can be updated again in a reverse direction so that all the choices become available again.This robustness of preference guarantees that if a player is able to control her emotion of anger before making a decision，she will be able to act in a normal way.

The rest of the paper is organised as follows.Section 2 gives a modal logic for modeling sequential games with anger.We first propose the semantics of our logic，modeling anger as update operators.Then we give its axiomatic system and prove the soundness and completeness of our logic with respect to its semantics.Section 3 shows what we can say by applying our logic to ultimatum games in which the responder is angry.Section 4 concludes the paper and suggests some future work.

2　Modal Logic for Sequential Games with Anger

First，we give the definition of sequential games.

Definition 1 AsequentialgameisatupleG=（W，R，N，Pl，｛ρi｝i∈N，wroot），where

1.W is the set of possible states in the game；

2.R is a binary relation on W，and（W，R）is a directed，irreflexive，and nontransitive tree with wrootas the root；

3.N is the set of players；

4.Pl:W→N assigns to each action point one player，who makes decision at that point；and

5.ρi:W→N assigns to player i a payoff at each possible state in W，for each i∈N.Specially，we require that for all w∈W and for all i∈N，min｛ρi（u）|u∈R（w）｝exists.

In this definition，wrootdenotes the beginning of the game G，which links to all states in W in finite steps via different choices of different players.It should benoticed that R is not transitive in our model.It means that instead of the concept of strategy，which in the context of sequential games normally denotes a whole set of choices a player makes in a game，R only models players'particular actions at certain stages of the game.This deviation from the traditional setting is in line with our definition of payoffs.

Anger is regarded as one of the visceral factors［6］，which generate behaviour that is short-sighted and beyond control［5］.According to［5］，visceral factors narrow people's attention of time towards the present，which means that angry people，when makingdecisions，arelikelytoignorelongtermpayoffandinsteadfocusonthepayoff that is immediately reachable.To model angry players'short-sighted decisions，we needplayers'short-termpayoff.Unlikethetraditionaldefinitionofsequentialgames，where players are only assigned payoffs to possible outcomes［9］，in our model players'payoffs are assigned to every node in the game tree.This definition of payoffs is in line with previous works in modal logic for games（for an example，see［4］）.Our assumptionisthatwhenplayersaresoangrythattheybecomeshort-sighted，theyonly focus on their opponents'payoffs that can be minimised by their next decision.Since the target player's minimal payoff is angry player's reference，we specially require the existence of minimal payoff for all the players within every stage.

Given a finite set of players Ag，a non-empty set of actions for all players Act=∪i∈AgActi，where Actiis the set of i's actions，and a countable set of atomic propositions At=｛p，q，r，...｝，the language LULA（At，Ag，Act）of our logic is generated by the following BNF：

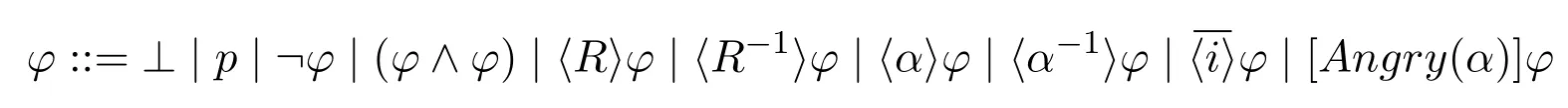
1.〈R〉φ reads“after one step of move，it is possible that φ is true”.

2.〈R-1〉φ reads“φ is true in the previous step”.

3.〈α〉φ reads“after choosing action α，φ is true”.

4.〈α-1〉φ reads“before choosing action α，φ is true”.

6.［Angry（α）］φ reads“when the player，who is making decision at the resulting state of α，is angry because of α，φ is true”.

Definition 2 Given a sequential game G=（W，R，N，Pl，｛ρi｝i∈N，wroot），a model derived from G for LULAis MG=〈W，R，｛Pi｝i∈Ag，S，V〉，where

2.S:Act→2Rmaps each action to a set of pairs in R，such that if α∈Acti，S（α）=｛（w1，w2）∈R|Pl（w1）=i｝；and

3.V:At→℘（W）is a valuation.

We write R（w）for the set of all R-successors of w，i.e.，R（w）=｛w′∈W|Rww′｝. Similarly，we write Pi（w）for the set of all Pi-successors of w，i.e.，Pi（w）=｛w′∈W|Piww′｝.Note that if w′∈Pi（w）then there exits w0∈W such that w，w′∈R（w0）.

We denote by Msg the class of all models derived from all sequential games. For any model M=〈W，R，P，S，V〉in Msg，it is easy to see that for all w∈W，Piis asymmetric and its complement is transitive on R（w），i.e.，for all x，y，z∈R（w），¬Pixy and¬Piyz implies¬Pixz.Moreover，（W，R）is a directed，irreflexive，and non-transitive tree，i.e.，

1.there exists wroot∈W such that all other w∈W can be reached from wrootby finite steps of R；

2.every w∈W except wroothas a unique R-predecessor；and

3.R is acyclic.

It can be verified that a model M=〈W，R，｛Pi｝i∈Ag，S，V〉satisfies the above properties if and only if it is a derived model from a sequential game.

Definition 3 Given a model M=〈W，R，｛Pi｝i∈Ag，S，V〉in Msg，the truth conditions for LULAare defined as follows：

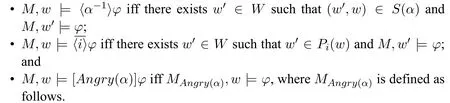
Definition 4 In M=〈W，R，｛Pi｝i∈Ag，S，V〉，if the action α（α∈Actj）makes the player moving on its resulting state angry，then the model M updates to MAngry（α）=〈W，R′，｛Pi｝i∈Ag，S′，V〉，where R′and S′are defined as follows：

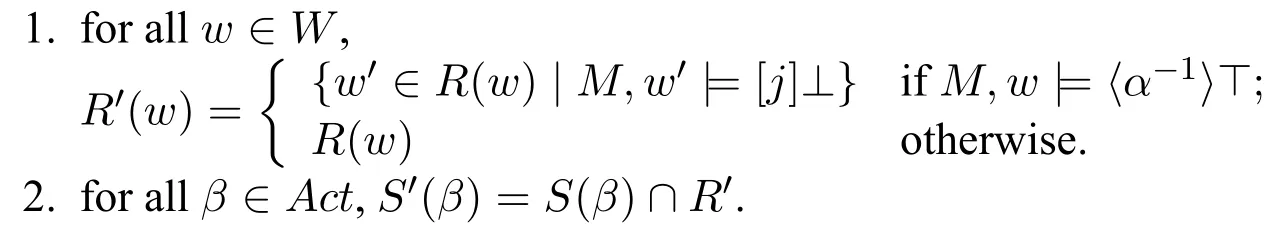
The update of our model means that if Player j's action α makes the following player i angry，then Player i's action set is restricted.While Player i's action set remains the same for the historic choices before α，her anger restricts her action set just following α，and the left over actions are those most unwanted by Player j.

Definition 5 We say that φ is valid in Msg，denoted⊨Msgφ，if for all M in Msg，for all w in M，M，w|=φ.

Theorem 1 For α∈Actj，the following reduction axioms are valid.

Proof 1. M，w |= ［Angry（α）］p ⇐⇒ MAngry（α），w |= p ⇐⇒ w ∈ V （p） ⇐⇒M，w|=p.

2.M，w|=［Angry（α）］¬φ⇐⇒MAngry（α），w|=¬φ⇐⇒MAngry（α），w/|=φ⇐⇒M，w/|=［Angry（α）］φ⇐⇒M，w|=¬［Angry（α）］φ.

3.M，w|=［Angry（α）］（φ∧ψ）⇐⇒MAngry（α），w|=φ∧ψ⇐⇒MAngry（α），w|=φ and MAngry（α），w|=ψ⇐⇒M，w|=［Angry（α）］φ and M，w|=［Angry（α）］ψ⇐⇒M，w|=［Angry（α）］φ∧［Angry（α）］ψ.

4.M，w|=［Angry（α）］〈R〉φ⇐⇒MAngry（α），w|=〈R〉φ⇐⇒there is u∈W such that u∈R′（w），and MAngry（α），u|=φ.There are two cases here：

·M，w|=¬〈α-1〉⊤，then we have an equivalent relation with：there exists u∈R（w），M，u|=［Angry（α）］φ⇐⇒M，w|=¬〈α-1〉⊤∧〈R〉［Angry（α）］φ；or

5.M，w|=［Angry（α）］〈R-1〉φ⇐⇒MAngry（α），w|=〈R-1〉φ⇐⇒there is u∈W such that w∈R′（u），and MAngry（α），u|=φ.There are two cases here：

·M，u|=¬〈α-1〉⊤，then we have an equivalent relation with：there exists u∈W，w∈R（u）and M，u|=［Angry（α）］φ⇐⇒M，w|=〈R-1〉（¬〈α-1〉⊤∧［Angry（α）］φ）；or

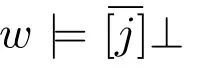
6&7.The proof for the reduction of［Angry（α）］〈β〉φ is similar to the proof for［Angry（α）］〈R〉φ，and the proof of［Angry（α）］〈β-1〉φ is similar to the proof for［Angry（α）］〈R-1〉φ.

·M，w0|=¬〈α-1〉⊤，then we have an equivalent relation with：

M，u|=［Angry（α）］φ⇐⇒M，w|=〈R-1〉¬〈α-1〉⊤∧〈i〉［Angry（α）］φ；

It follows from Theorem 1 that every formula in LULAcan be reduced to a formula without update operators.

Definition 6 The Update Logic of Anger，denoted ULA，is given by the following axiomatic system，in addition to the above reduction axioms：

1.K and GEN（generalization）for all modalities，MP（modus ponens），and US（uniform substitution）；

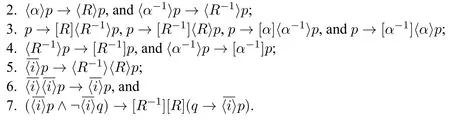
Theorem 2 ULA is sound with respect to Msg，i.e.，for all φ∈LULA，⊢ULAφ implies⊨Msgφ.

Proof It suffices to verify that all axioms of ULA are valid in Msg and all rules of ULA preserve validity.The only interesting cases are those axioms from item 2 to 7 above.Given any model M=〈W，R，P，S，V〉in Msg，since S is a mapping into R，it is easy to see that〈α〉p→〈R〉p and〈α-1〉p→〈R-1〉p are true in M. Since R-1is the converse of R，it is easy to see that both p→［R］〈R-1〉p，and p→［R-1］〈R〉p are valid.The validity of p→［α］〈α-1〉p and p→［α-1］〈α〉p is analogous.The fact that every w∈W has at most 1 R-predecessor guarantees the validity of〈R-1〉p→［R-1］p and〈α-1〉p→［α-1］p.

To prove the completeness of ULA，we define the canonical model for ULA as follows.

Definition 7 The canonical model for ULA is

where

1.Wcis the set of all maximal consistent sets（MCSs）of ULA；

2.for all u，v∈Wc，v∈Rc（u）if for all φ，φ∈v implies〈R〉φ∈u；

3.for all u，v∈Wc，u∈R-1，c（v）if for all φ，φ∈u implies〈R-1〉φ∈v；

5.for all α∈Act and u，v∈Wc，（u，v）∈Sc（α）if for all φ，φ∈v implies〈α〉φ∈u；

6.for all α∈Act and u，v∈Wc，（v，u）∈S-1，c（α）if for all φ，φ∈v implies〈α-1〉φ∈u；and

7.Vc（p）=｛w∈Wc|p∈w｝.

Proposition 1 For all u，v in the canonical model Mc，we have v∈Rc（u）iff u∈R-1，c（v）.

Proof Suppose φ∈u，and v∈Rc（u）.By the axiom p→［R］〈R-1〉p，we have［R］〈R-1〉φ∈u.By v∈Rc（u），it follows that〈R-1〉φ∈v，which in turn implies u∈R-1，c（v）.The proof of the other direction is symmetric.□

A similar proposition for the relationship between Scand S-1，ccan be proved analogously.

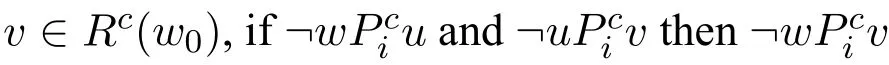
Definition 8 A network is a tupple N=（N，R，｛Pi｝i∈Ag，S，ν），where

4.ν is a labelling function mapping each point in N to a MCS.

Definition 9 A network N=（N，R，｛Pi｝i∈Ag，S，ν）is coherent if：

1.（N，R）forms a directed，irreflexive，and non-transitive tree；

2.for all s，t∈N，t∈R（s）implies ν（t）∈Rc（ν（s））；

3.for all α∈Act and s，t∈N，（s，t）∈S（α）implies（ν（s），ν（t））∈Sc（α）；

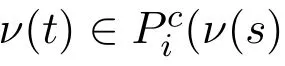
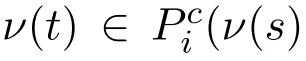
（c）for all w∈N，Piis asymmetric on R（w），and for all x，y，z∈R（w），¬Pixy and¬Piyz implies¬Pixz.

For proving weak completeness of ULA，we define the saturation of a network for any formula φ∈LULA.For any φ∈LULA，let Sub（φ）be the set of all subformulas of φ.

Definition10 Givenanyformulaφ0∈LULA，anetworkN=（N，R，｛Pi｝i∈Ag，S，ν）is saturated for φ0if：

1.for all〈R〉φ∈Sub（φ0），if〈R〉φ∈ν（u），then there exists v∈N such that φ∈ν（v）and v∈R（u）；

2.for all〈R-1〉φ∈Sub（φ0），if〈R-1〉φ∈ν（u），then there exists v∈N such that φ∈ν（v）and u∈R（v）；

3.for all〈α〉φ∈Sub（φ0），if〈α〉φ∈ν（u），then there exists v∈N such that φ∈ν（v）and（u，v）∈S（α）；

4.for all〈α-1〉φ∈Sub（φ0），if〈α-1〉φ∈ν（u），then there exists v∈N such that φ∈ν（v）and（v，u）∈S（α）；and

A network is perfect for φ0，if it is both saturated for φ0and coherent.

Definition 11 Given any network N=（N，R，｛Pi｝i∈Ag，S，ν），the induced model of N is MN=（N，R，P，S，VN），where for w∈N，

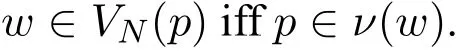
Lemma 1（Truth Lemma）For any induced model MNof a perfect network N for φ0，for all φ∈Sub（φ0），we have：

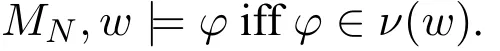
Proof We prove by induction on φ.

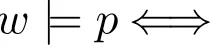
2.The case when φ is¬ψ or ψ1∧ψ2is trivial.

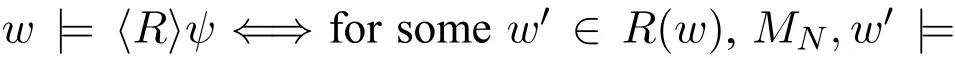
For the last equivalence relation，the left to right direction is established by the coherence of N，and that N is saturated for φ0proves the right to left direction.

Definition 12 For any network N=（N，R，P，S，ν），we say that N has a defect if at least one of the following cases is true：

1.（S1-defects）there exists s∈N such that there exists〈R〉φ∈ν（s）but there does not exists t∈N such that t∈R（s）and φ∈ν（t）；

2.（S2-defects）there exists s∈N such that there exists〈R-1〉φ∈ν（s）but there does not exists t∈N such that s∈R（t）and φ∈ν（t）；

3.（S3-defects）there exists α∈Act and s∈N such that〈α〉φ∈ν（s）but there does not exists t∈N such that（s，t）∈S（α）and φ∈ν（t）；

4.（S4-defects）there exists α∈Act and s∈N such that〈α-1〉φ∈ν（s）but there does not exists t∈N such that（t，s）∈S（α）and φ∈ν（t）；

Lemma 2（Repair Lemma）For any defect of a finite coherent network N，there is a finite coherent extension N′lacking this defect.

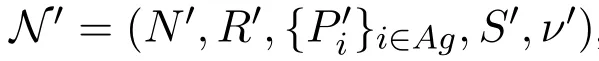
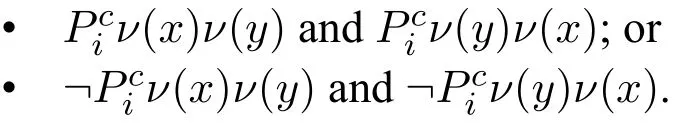
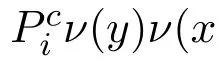
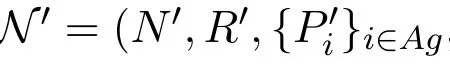
Since t/∈N，to show that（N′，R′）forms a directed，irreflexive，and non-transitive tree it is sufficient to show that there does not exists t′∈N such that s∈R（t′）and that t is the root of（N′，R′）.Given that〈R-1〉φ∈ν（s），by the axiom〈R-1〉p→［R-1］p，we have［R-1］φ∈ν（s）.It means that if there exists t′∈N such that s∈R（t′），then it must be φ∈ν（t′）.But this is contradictory to the existence of the S2-defect.

Since（N，R）is a tree and s∈N does not have a predecessor，it is easy to see that s is the root of（N，R）.It means that s links to all nodes in N via R，and since t is the only point in N′that links to s via R′，t is the only point that links to all the points in N′via R′.Hence，t is the root of（N′，R′）.Other conditions for coherence is trivial.

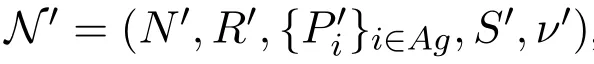
With the axiom of〈α〉p→〈R〉φ，it is easy to show that ν（t）∈Rc（ν（s））.The proof of other coherence conditions is similar to that in S1-defects.

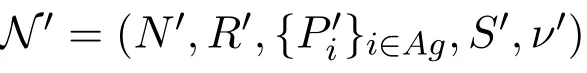
With the axiom of〈α-1〉p→〈R-1〉φ，it is easy to show that ν（s）∈Rc（ν（t））.The proof of other coherence conditions is similar to the proof for repairing S2-defects.

Proposition 2 shows that Σ∈Rc（ν′（w）），and the proof of other coherence conditions is similar to that in repairing S1-defects.□

Theorem 3 ULA is weakly complete with respect to Msg，i.e.，for all φ∈LULA，⊨Msgφ implies⊢ULAφ.

Proof Choose some set S=｛si|i∈N｝，and given any ULA-consistent formula φ0，enumerateallpotentialdefectsforφ0withSub（φ0）×S.ByLindenbaum'slemma we know that φ0can be extended to a maximal ULA-consistent set Σ+.Define N0=（｛s0｝，∅，∅，∅，∅，｛（s0，Σ+）｝），which is obviously finite and coherent.Suppose for n≥0，Nn=（Nn，Rn，Sn，｛Pni｝i∈Ag，Sn，νn）is finite and coherent，and D is the defectofNnthatisminimalinourenumeration.ByRepairLemma，thereexistsNn+1extending N lacks the defect of D.Let N=（N，R，｛Pi｝i∈Ag，S，ν）be defined as follows：

Since Sub（φ0）is finite，we can have a perfect network for φ0within finite steps.Let MNbe the induced model of N，then MNis in Msg.By Truth Lemma，we have MN，s0|=φ0.□

We are going to show that ULA is not strongly complete.

Proposition 5ULA is not strongly complete with respect to Msg，i.e.，there exists a set of ULA-consistent formulas Γ such that there does not exist any M∈Msg，and any w∈M such that M，w|=Γ.

Proof Consider Γ=｛φn|n∈ω，and φn=〈R-1〉φn-1，and φ0=⊤｝.To show that Γ is consistent，it is sufficient to show that any finite subset Ψ of Γ is consistent.For any Ψ，there exists m∈ω such that Ψ⊆｛φn|n≤m，and φn=〈R-1〉φn-1，and φ0=⊤｝=Φ，and the consistency of Φ shows that Γ is consistent. Letbe the conjunction of all formulas in Φ.We are going to show that¬is not valid，i.e.，there exists M∈Msg，and w∈M such that M，w|=.

LetM=〈W，R，∅，∅，∅〉，whereW=｛w1，...，wm｝，andR=｛（wn-1，wn）| n≤m｝.It is easy to see that M∈Msg，and M，wm⊨.

Now，suppose ULA is strongly complete with respect to Msg，i.e.，there exists M′∈Msg，and w∈M′such that M′，w|=Γ.But this is impossible，because by M′，w|=Γ，wecaninductivelydefineaninfiniteR-1pathstartingfromw.However，sinceM′∈Msg，theremustexistsarootinM′andthusM′cannotcontainaninfinite R-1path.Hence，ULA is not strongly complete with respect to Msg.□

3　Application

In this section，we apply our logic to the context of ultimatum games.We are going to show that if the responder is angry towards a proposal，then in most cases she will reject the proposal and both players will get nothing from the game，but there is also one case where the responder may accept the proposal.

An ultimatum game is a two-player game where the proposer first gives a proposalonthesharingofacertainamountofmoney，thentheresponderdecideswhether to accept this proposal or not.A proposal contains a natural number n（n≤100），which indicates the percentage of money the proposer is sharing to the responder. If the responder accepts a proposal of n，she receives n%of the money while the proposer gets the rest（100-n）%.If the responder rejects a proposal，then both players receive nothing from the game.A graphic presentation of the ultimatum game is shown in Figure 1.

Our modal language for the ultimatum game is L（At，Ag，Act），where At=｛pn|n∈［0，100］｝∪｛prej｝，Ag=｛Pro，Res｝，and Act=｛propose，n|n∈［0，100］｝∪｛acc，rej｝.The primitive formulas pnis the payoff profile of（（100-n）%，n%），and prejequals（0，0）.The proposer and the responder of the game aredenoted by Pro and Res in Ag，respectively.The action of“propose，n”means the proposer proposes n%of share for the responder，and“acc”and“rej”refer to the responder's action of“accept”and“reject”，respectively.Then given any ultimatum game G=〈W，R，N，Pl，｛ρi｝i∈N，wroot〉，we can generate our model MG=〈W，R，｛Pi｝i∈Ag，S，V〉.

Figure 1：Ultimatum Game Before Angry Update

Figure 2：Ultimatum Game After Angry Update（n∈［0，99］）

Then，suppose the responder is angry towards a proposal of n%（0≤n＜100）. According to Definition 4，the angry update restricts the responder's action set according to the proposer's preference，and only the action leading to lowest payoffs for the proposer remains.Thus，in the case of 0≤n＜100，the only action left after the angry update is“Reject”.Because M，wn|=［acc］⊥in Figure 2，we have M，wroot|=〈propose，n〉［Angry（propose，n）］［acc］⊥.

Summarising the above discussion，we have

1.for n=0，M，wroot|=〈propose，n〉［Angry（propose，n）］［acc］⊥，

2.for 1≤n≤99，

3.for n=100，

4　Conclusion

In this paper，we model angry players'short-sighted and irrational behaviour in sequential games by a modal logic with update operators.When a player gets angry towardsachoiceofanotherplayer，ourmodelupdatessothatonlythoseactionswitha most unwanted outcome of the targeted player remain available for the angry player. We construct an axiomatic system for the logic and prove its soundness and weak completeness.Finally，we apply the logic to ultimatum games in which the responder is angry.Since angry updates do not force an action in some cases，it would be interesting to see the combination of different kinds of rationalities［3］and preference updates［10］with angry updates in the future.

References

［1］C.Adam，A.Herzig and D.Longin，2009，“A logical formalization of the occ theory of emotions”，Synthese，168（2）：201-248.

［2］J.R.Averill，1982，Anger and aggression:An essay on emotion，New York：Springer.

［3］J.Cui and X.Luo，2013，“A unified epistemic analysis of iterated elimination algorithmsfromregretviewpoint”，Logic，Rationality，andInteraction，pp.82-95，Springer.

［4］P.Harrenstein，W.Van der Hoek，J.-J.Meyer and C.Witteveen，2003，“A modal characterization of nash equilibrium”，Fundamenta Informaticae，57（2-4）：281-321.

［5］G.Loewenstein，1996，“Out of control：Visceral influences on behavior”，Organizational Behavior and Human Decision Processes，65（3）：272-292.

［6］G.Loewenstein，2000，“Emotions in economic theory and economic behavior”，The American Economic Review，90（2）：426-432.

［7］M.M.Pillutla and J.K.Murnighan，1996，“Unfairness，anger，and spite：Emotional rejections of ultimatum offers”，Organizational Behavior and Human Decision Processes，68（3）：208-224.

［8］A.G.Sanfey，J.K.Rilling，J.A.Aronson，L.E.Nystrom and J.D.Cohen，2003，“The neural basis of economic decision-making in the ultimatum game”，Science，300（5626）：1755-1758.

［9］R.Selten，1975，“Reexamination of the perfectness concept for equilibrium points in extensive games”，International Journal of Game Theory，4（1）：25-55.

［10］J.Van Benthem，2007，“Dynamic logic for belief revision”，Journal of Applied Nonclassical Logics，17（2）：129-155.

［11］G.A.Van Kleef，C.K.De Dreu and A.S.Manstead，2004，“The interpersonal effects ofangerandhappinessinnegotiations”，JournalofPersonalityandSocialPsychology，86（1）：57.

2016-05-12

*The second author was supported by the Fundamental Research Funds for the Central Universities（No.13WKPY71）.