点到直线距离公式的研究性学习成果

桂　弢

(江苏省清河中学 　223001)

1　问题的提出

已知平面上的点P(x0,y0)，直线l:Ax+By+C=0(A,B不全为0)， 求点P到直线l的距离d.

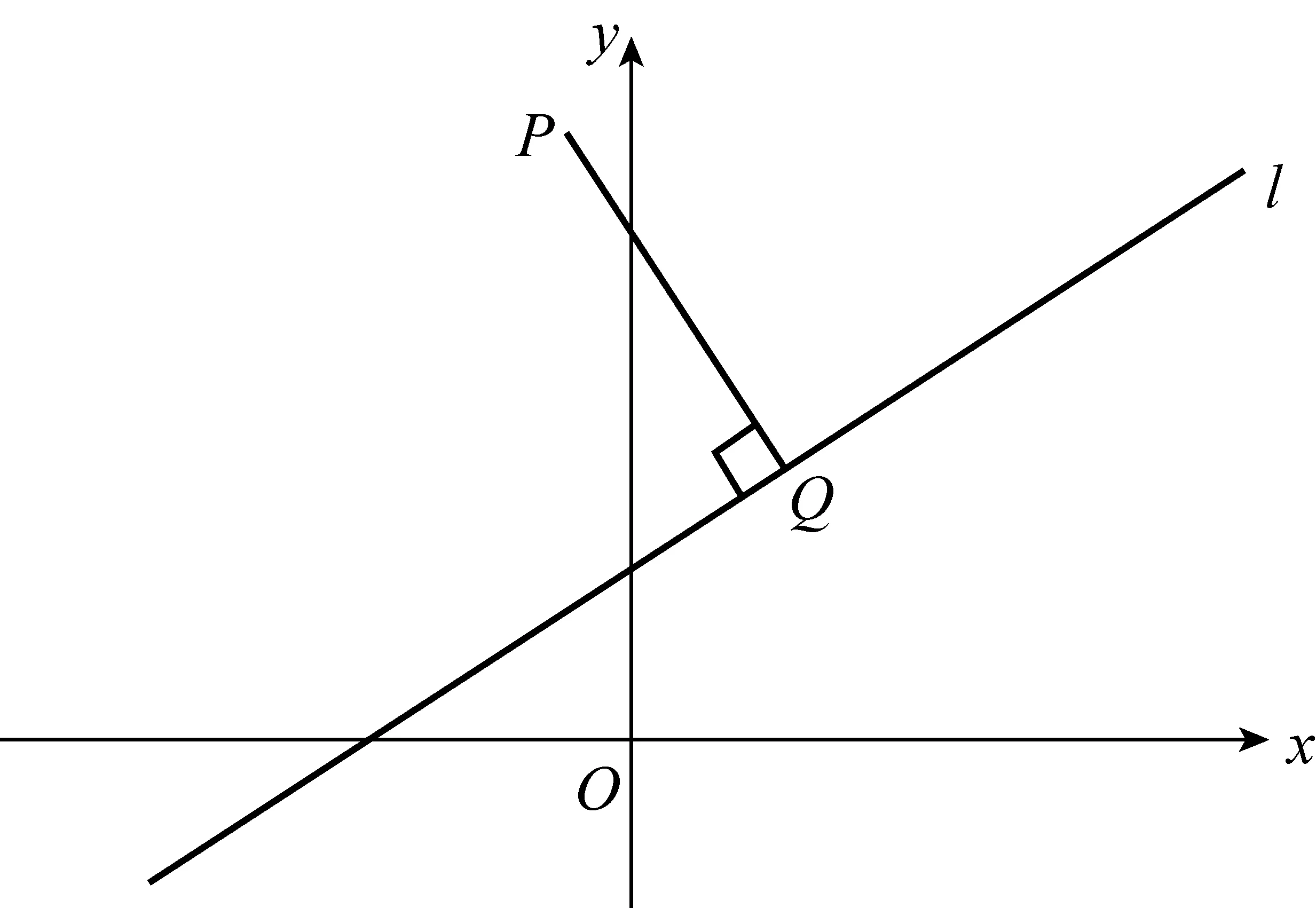
图1

对于直线l:Ax+By+C=0(A≠0,B≠0)外一点P(x0,y0)，过点P作PQ⊥l，垂足为Q. 过点P分别作x轴、y轴的平行线，交l于点M(x1,y0),N(x0,y2).

由Ax1+By0+C=0,Ax0+By2+C=0，得

PQ是Rt△PMN斜边上的高，由三角形面积公式可知

当A=0或B=0时，此式仍然成立.

图2

为什么要选择等面积法呢？ 教学参考书是这样解释的：定义法是常规方法，思路比较清晰，但计算量较大；一般情况下，点到直线距离公式的推导是采用等面积法的思路.

不少教师教学时也是这样说和这样做的，这不禁让人产生几点疑惑：

1.定义法真的计算量较大吗？一个例子就能说明这一问题吗？

2.除了这两种方法外，是否还有其他的推导方法或更简洁的推导方法呢？

带着这些问题，笔者设计了一次研究性学习活动，专门安排学生探究点到直线距离公式的推导. 放开手后，发现学生的创造力是巨大的，给出了不少新颖的推导方法. 现将学生的智慧结晶以及本人的一些思考整理出来介绍给大家，欢迎指正.由于特殊情形A=0或B=0对一般结论总是成立的，为了行文简洁，下面只研究A≠0,B≠0的情形.

2　多视角探究，彰显联系

唯物辩证法认为事物是普遍联系的. 所谓联系，是指事物之间以及事物内部诸要素之间的相互依赖、相互影响、相互制约和相互作用. 联系具有普遍性、客观性和多样性. 用联系的观点看问题，可以让我们的视野更开阔，看问题也更全面，联系也是数学的本质之一. 对于点到直线距离公式的推导，可以从多个角度进行探究，这正体现了不同数学模块之间的内在联系.

2.1　定义的视角

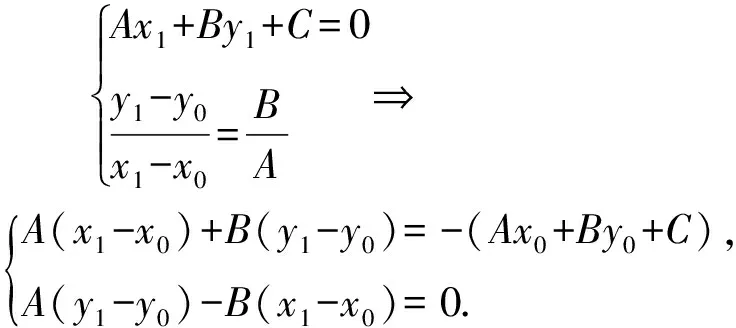
将两式分别平方并相加，得

(A2+B2)[(x1-x0)2+(y1-y0)2]

=(Ax0+By0+C)2,

点评由此可见，对于定义法，若用一般形式来处理，则其运算量可以比具体问题小很多.

2.2　轴对称的视角

作出点P关于直线l的对称点R，要求点P到直线l的距离，就是要先求出PR的长，然后再除以2即可，做法也很简洁.

解析设点P(x0,y0)关于直线l的对称点为R(m,n)，则

将两式分别平方并相加，得

(A2+B2)[(m-x0)2+(n-y0)2]

=4(Ax0+By0+C)2，

点评此推导方法是一种迂回的做法，它与定义法有异曲同工之妙.

2.3　向量的视角

由于两点间的距离公式是可以利用向量来推导的，那么点到直线的距离公式能否用向量来推导呢？不少学生产生了这样的想法，回答是肯定的.

于是点P到直线l的距离

点评该推导方法简洁明了，令人称奇. 可见，向量是一种很重要的数学工具.

2.4　函数的视角

由于点P到直线l的距离就是点P到直线l上任意一点的距离的最小值，故可以通过建立目标函数，利用求二次函数的最小值来推导点到直线的距离公式，方法常规，想法自然，但对学生的运算能力有较高要求.

PM2=(x-x0)2+(y-y0)2

点评函数是中学数学的主要内容，建立目标函数解题则是一种很重要的数学思想方法.

2.5　不等式的视角

设a,b,c,d均为实数，则(a2+b2)(c2+d2)≥(ac+bd)2，等号当且仅当ad=bc时成立. 这是柯西不等式的二维形式，利用这一不等式，可以轻松地推导出点到直线的距离公式.

解析设M(x,y)是直线l上任意一点，则

PM2=(x-x0)2+(y-y0)2，

由柯西不等式，得

(A2+B2)[(x-x0)2+(y-y0)2]

≥[A(x-x0)+B(y-y0)]2，

即(A2+B2)[(x-x0)2+(y-y0)2]

≥(Ax+By-Ax0-By0)2=(-Ax0-By0-C)2，

所以

当且仅当A(y-y0)=B(x-x0)，

即PM⊥l时，取等号.

点评此方法的产生源于对点到直线距离公式结构特征的细心观察和广泛联想.

2.6　解三角形的视角

构造直角三角形，将点P到直线l的距离d和直线l的倾斜角α或角π-α置身其内，这是多数学生想到的方法. 构造直角三角形的方法有多种，如过点P作直线l的平行线，构造斜边在x轴或y上的直角三角形等，下面仅介绍一种.

解析设直线l:Ax+By+C=0的倾斜角为α，过点P作PQ⊥l，垂足为Q. 过点P作x轴的垂线，交l于点M(x0,y1).

在Rt△PQM中，当α为锐角时，∠MPQ=α；当α为钝角时，∠MPQ=π-α.

于是d=PQ=PM·cos∠MPQ=PM·|cosα|

点评这种构造直角三角形的方法较为普遍，但会忽视对倾斜角α的讨论.

图3

3适当推广，凸现发展

唯物辩证法认为事物不仅是普遍联系的，而且是永恒发展的. 发展的实质是指事物的前进和上升，新事物的不断产生. 联系的观点和发展的观点都是我们认识和观察事物的基本方法. 利用发展的观点看问题，会让我们的思维更活跃，想象力更丰富，数学也是一门不断发展的科学. 在研究性学习活动中，既要培养学生分析问题和解决问题的能力，也要培养学生从数学角度发现问题和提出问题的能力. 为此，笔者还启发学生进行类比、联想和猜想，尝试将二维问题向三维空间拓展，研究空间中的点到平面的距离问题.

问题已知空间内的点P(x0,y0,z0)，平面α:Ax+By+Cz+D=0(A，B，C不全为0)，求点P到平面α的距离d.

下面采用向量法进行研究.

设点Q(x1,y1,z1)为点P在平面α上的射影，则Ax1+By1+Cz1+D=0. 因为

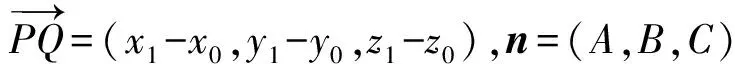
4　结束语

从上可以看出，点到直线距离公式的推导方法是很多的，不少方法十分简洁，也来自于学生. 可见，如果我们总是盲信教材，缺乏批判精神，就失去了激发学生创造力、培养学生核心素养的机会，教学也始终是浅层次的. 无论是教师还是学生，对待教材的态度是既要尊重它，但又不能迷信它，要有自己的思考，要敢于质疑教材的编写，这才是科学的态度，这对教师的专业成长和学生的能力发展也都是有益的.