薄壁梁剪切挠曲性能解耦分析方法研究

周茂定，蔺鹏臻，张元海

(1.甘肃农业大学 土木工程系，甘肃 兰州 730070；2.兰州交通大学 土木工程学院，甘肃 兰州 730070)

薄壁梁结构广泛应用于现代桥梁及结构工程中,剪切变形作为其挠曲力学特性的重要影响因素一直受国内外学者的广泛关注。文献[1-12]论述了关于T形、箱形薄壁梁的剪力滞、剪切变形等相关研究成果。这些研究文献中常采用翼板位移差函数作为广义位移来分析薄壁结构的剪力滞效应[2-6],部分学者[7-9]通过引入Timoshenko梁理论来反映薄壁梁的腹板剪切变形。翼板剪力滞[4]和腹板剪切变形[7]本质均是由壁板的面内剪切变形引起,可统称为剪切效应。在分析剪切广义位移时,文献[2-12]常将其与初等梁挠曲混为一起,导致分析过程相对复杂。文献[13-16]选取剪切引起的挠度作为独立变形状态,使得薄壁结构的剪切挠曲分析具有明确的物理意义,但分析过程仍以能量变分法[4-16]为基础。利用该法获得广义位移的控制微分方程多为复杂的高次方程。同时,该法也很难适用连续梁的剪切挠曲分析,导致该法不能广泛应用于实际工程。我国JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》[17]采用有效宽度来考虑T形及箱形梁的剪力滞效应。该方法虽然分析简便,但不能精确获得挠曲应力沿翼板的实际分布,也不能获得薄壁梁的精确挠度。因此还需寻求适合工程应用且精度较高的简化分析方法。文献[11-13]在研究箱梁悬臂板和顶板剪力滞翘曲位移时发现两者剪应变存在一定差异,进而导致剪切翘曲应力的求解不够准确。遗憾的是上述文献并未明确给出翘曲应力修正的表达式。

本文从薄壁梁各壁板的应变与位移关系出发,建立一种具有明晰力学机理的挠曲位移函数。选取剪切挠度为广义位移,通过解耦挠曲性能建立剪切挠度及剪切翘曲应力的简化分析公式,并给出翼板翘曲应力的合理修正公式。然后,利用中支点变形连续条件导出薄壁连续梁的简化分析方法。最后通过数值算例验证本文方法的有效性及求解精度。

1 薄壁梁截面剪切挠曲函数分析

1.1 坐标系及基本假设

选取受任意荷载p(z)的简支对称工字梁结构见图1,采用正交直角坐标系,x和y轴为横截面的形心主轴,z轴为梁纵轴。对于组成薄壁梁截面的各壁板,可认为其应力沿壁厚均匀分布。因此,建立沿各壁板中心线的流动坐标系n-s-z,流动坐标s以顺时针方向为正,n为各平面的法向坐标,见图1(b)。图1(b)中,a、b表示工字梁上、下翼板的半宽;ha、hb为形心至上、下翼板厚中心的距离;h为梁高;t为截面各壁厚度。

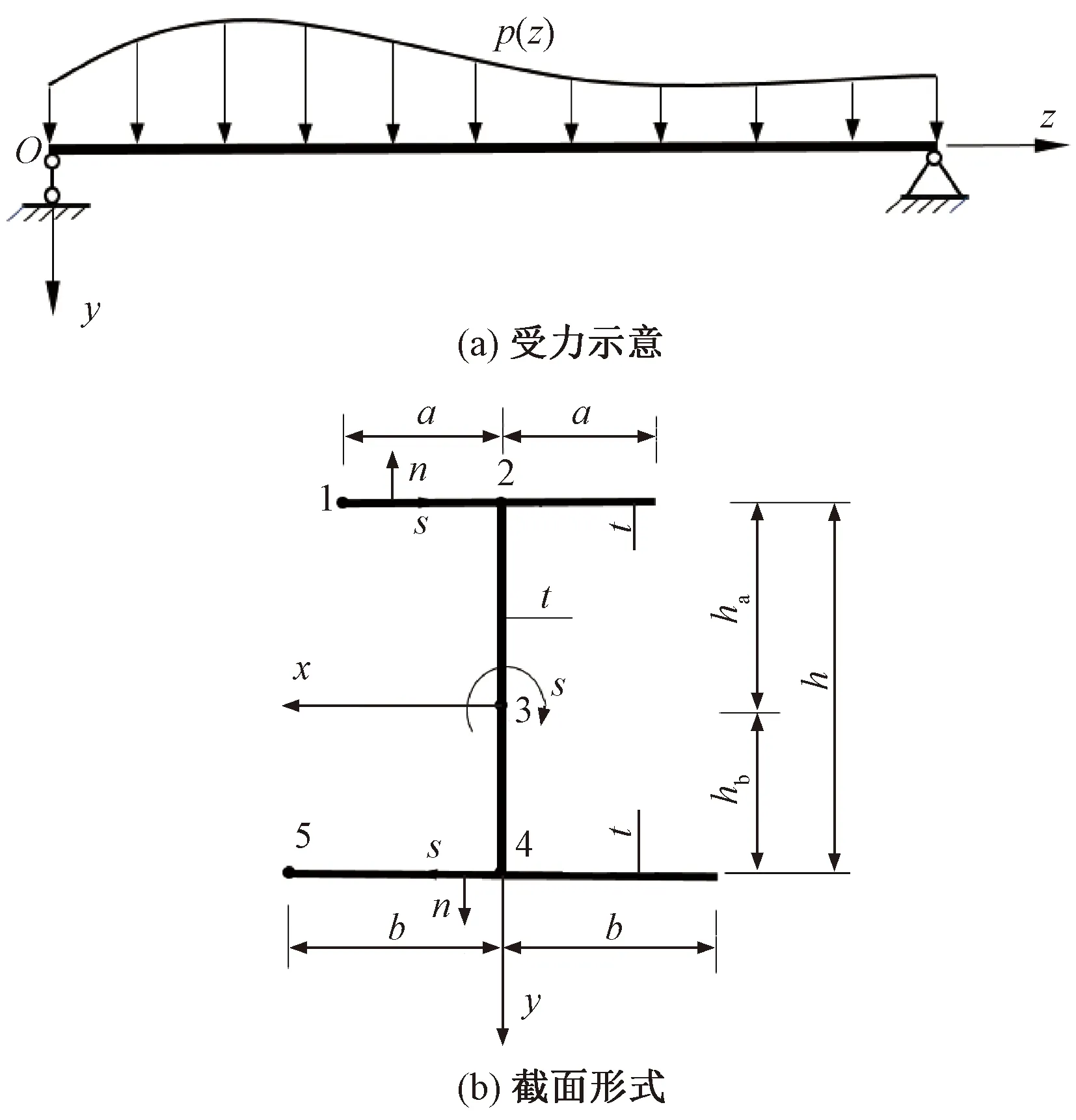
图1 受均布荷载的简支梁

在小变形条件下,薄壁梁截面保持刚性不变形[17],忽略各壁板的面外剪切变形和正应力。若用u表示z轴位移,v表示周向s轴位移,基于上述假设可知,截面各壁板将满足弹性理论中的平面应力方程[18]。因此,各壁板平面内的位移分量与变形分量之间关系为[18]

( 1 )

( 2 )

式中:εz为梁轴向应变;γsz为各壁板的面内剪切应变。

1.2 考虑剪切变形影响的挠曲分析

对于薄壁梁翼板,由截面的刚性不变形可知v沿z轴保持不变,即∂v/∂z=0。根据剪应力表达式及式( 2 )可得分别由u2(z)与u4(z)表示的工字梁上、下翼板的纵向位移ua、ub[10,15]表达式分别为

( 3 )

( 4 )

显然,u2(z)和u4(z)点也是腹板顶、底部的纵向位移。根据薄壁梁弯曲理论[17]可求得工字梁腹板3点(形心处)的剪应力为

( 5 )

式中:A为薄壁梁截面面积;Aa为梁上翼板面积;α1为腹板剪切系数。

由式( 5 )可得腹板的任意点的剪应力τw为

( 6 )

由式( 2 )与式( 6 )可求得梁腹板的剪应变γw为

( 7 )

若令w1(z)表示薄壁梁考虑剪切变形影响的竖向位移,则w′1(z)=∂v/∂z。从3点起对式( 7 )关于s进行积分,并转化为y坐标可得腹板的纵向挠曲位移uw为

( 8 )

式中:α2称为腹板翘曲系数,α2=1/(3A);u3(z)为积分起点常数。

显然,由式( 8 )可表示纵向位移u2(z)和u4(z)。综合式( 3 )、式( 4 )及式( 8 ),可求得薄壁梁截面的挠曲纵向位移u的表达式为

u(x,y,z)=-yw′1(z)+[α1y-α2y3+α3(x)]·

( 9 )

式中:α3(z)称为翼板剪切翘曲函数,其表达式为

(10)

式( 9 )为考虑剪切变形影响时,薄壁梁截面的纵向位移函数。对于单轴对称的薄壁箱梁[15-16]、T梁考虑剪切变形的位移函数分析过程与工字梁相同,在此不在赘述。

2 截面平衡条件分析

梁的竖向位移分解见图2。若将梁的挠曲位移w1(z)分解为初等梁挠曲w0(z)与剪切挠曲ws(z)两种变形状态,则有

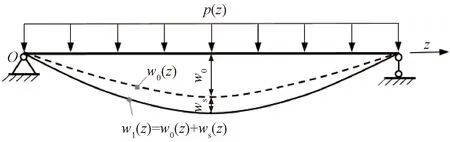
图2 梁的竖向位移分解

w1(z)=w0(z)+ws(z)

(11)

将式(11)代入式( 9 )中,再由式( 1 )及胡可定理可得梁截面的正应力σ为

σ(x,y,z)=-yEw″0(z)-yEw″s(z)+[α1y-α2y3+

(12)

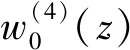
显然,式(12)右端第1项为初等梁理论下截面的正应力σ0。若仍保持w0满足初等梁理论下挠曲内力平衡,则σ0沿全截面不合成轴力,且σ0以y为力臂合成截面的弯矩M。因此,式(12)右端其余项则为剪切翘曲应力σs,其沿截面不合成轴力,且以y为力臂不合成力矩,即

yEw″s(z)+Eu′3(z)

(13)

(14)

(15)

将式(13)代入式(14)中化简整理后可得

(16)

式中:α41与α42分别称为腹板与翼板剪切修正系数,其表达式为

(17)

(18)

其中,Ab为下翼板的面积。

式(16)两边关于z积分便可求得含有积分常数的u3(z)表达式,而由于弹性小变形假设忽略梁轴线伸长,即截面不产生刚体位移,因而积分常数为0。将式(16)代入式(13)后,再代入式(15)可得

(19)

式中:系数λ=Ix/Iyα,Ix为梁截面惯性矩,Iyα可称为剪切惯性积,其表达式为

(20)

根据式(19)的关系,结合式( 9 )可得剪切翘曲纵向位移us为

us(x,y,z)=-ω(x,y)w′s(z)

(21)

式中:ω(x,y)为剪切翘曲位移函数,ω(x,y)=y-λα(x,y),α(x,y)=yα1-y3α2+α3(x)+α4。

对于其他单轴对称的箱形、T形面分析过程与工字梁相似,差异为截面参数值的不同。

3 简化分析方法及翘曲应力的修正

求解剪切挠曲位移的经典方法是根据式(21)及能量变分法[4-16]可导出ws的控制微分方程为

(22)

式中:k为剪切常数,其表达式为

(23)

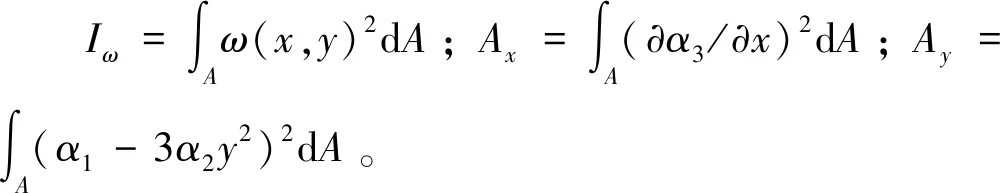
3.1 静定梁的简化分析方法

剪切翘曲控制微分方程式(22)的求解相对复杂,且由于解析表达式较为复杂,对连续梁很难得到解析式,而限制其工程应用。因此,本文将提出新的简化分析方法。

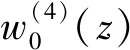
(24)

式中:μ为泊松比,由E/(2G)=1+μ得出。

根据式(19)及其与截面纵向位移的关系积分可得截面的剪切挠度ws为

(25)

式中:D为积分常数,需根据薄壁梁剪切挠度ws的边界条件确定。

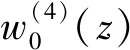
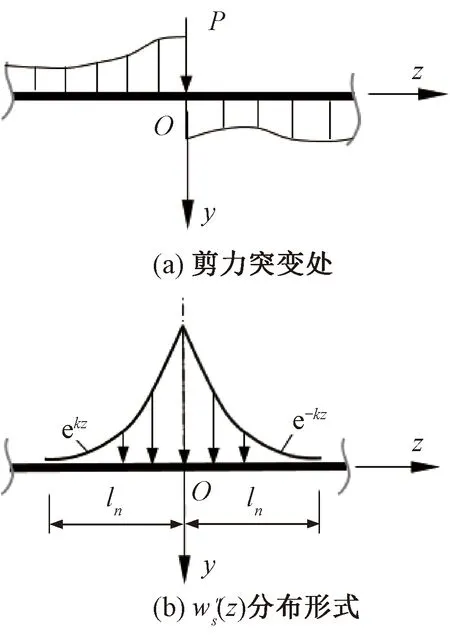
图3 剪力不连续点等效分析

在分析剪切挠曲变形状态时,将图3(a)中的集中荷载P转化为分布荷载p(z)分析。通过分析挠曲微分方程式(22)的解可知[14-15],w″s(z)在剪力不连续点分别以ekz和e-kz的形式对称分布于P的两侧(如图3(b)所示)。而由式(24)可知,p(z)的分布形式将与w″s(z)相同,设P的等效分布荷载集度为

p(z)=βPe-kz。

(26)

式中:β为分布荷载集度系数。

由于工程常用梁的等效分布荷载的主要影响范围ln较小,梁长相对ln可近似认为是∞。对y轴以右的分布荷载进行积分必然为合力P/2,从而可求得β为0.5k,从而可求得剪力不连续点的等效分布荷载。

3.2 连续梁的简化方法

对图4(a)所示的多跨连续梁,中支点的剪切支反力即为剪力不连续点的集中荷载P1-i(i=1,2,…)见图4(b)。值得注意的是,剪切支反力与初等梁的支反力不同。在结构力学中求解P1-i的常用方法是根据连续梁中支点剪切挠度ws为0的条件,列方程组求解各支点的剪切反力,从而求解进一步分析剪切变形。

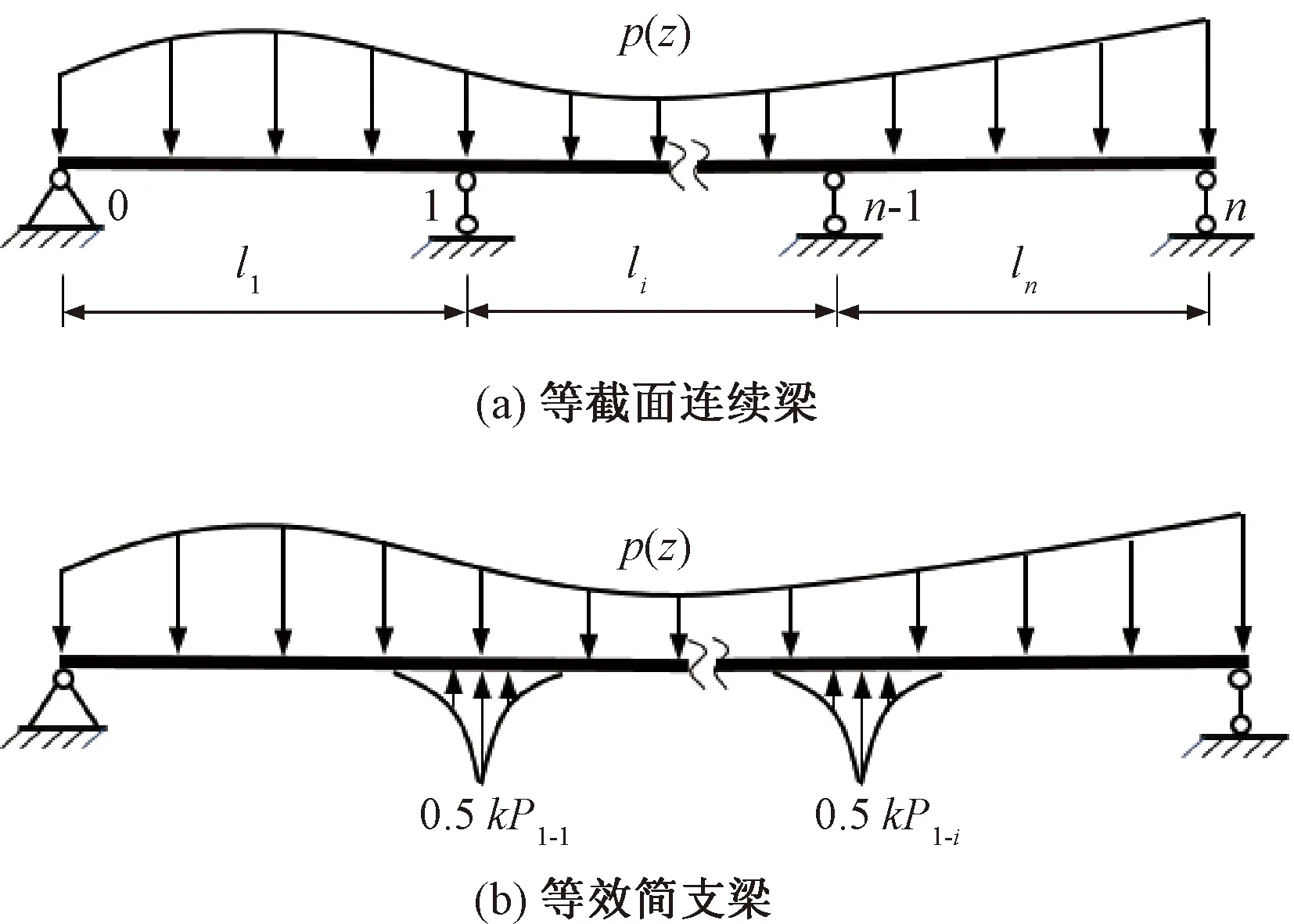
图4 连续梁中支点的等效转换

然而,上述分析方法涉及复杂方程组的求解,分析过程十分复杂。由式(25)可知,连续梁边支点剪切挠度为0,使得积分常数D必然为0。因此,在中支点处ws=0的条件将转化为该点的弯矩为0,进而连续梁的剪切挠曲将转为多跨简支梁形式,见图5(a)。当忽略剪切支反力P1-i的分布荷载对梁弯矩影响时,可近似为图5(b)所示简支梁进行分析。

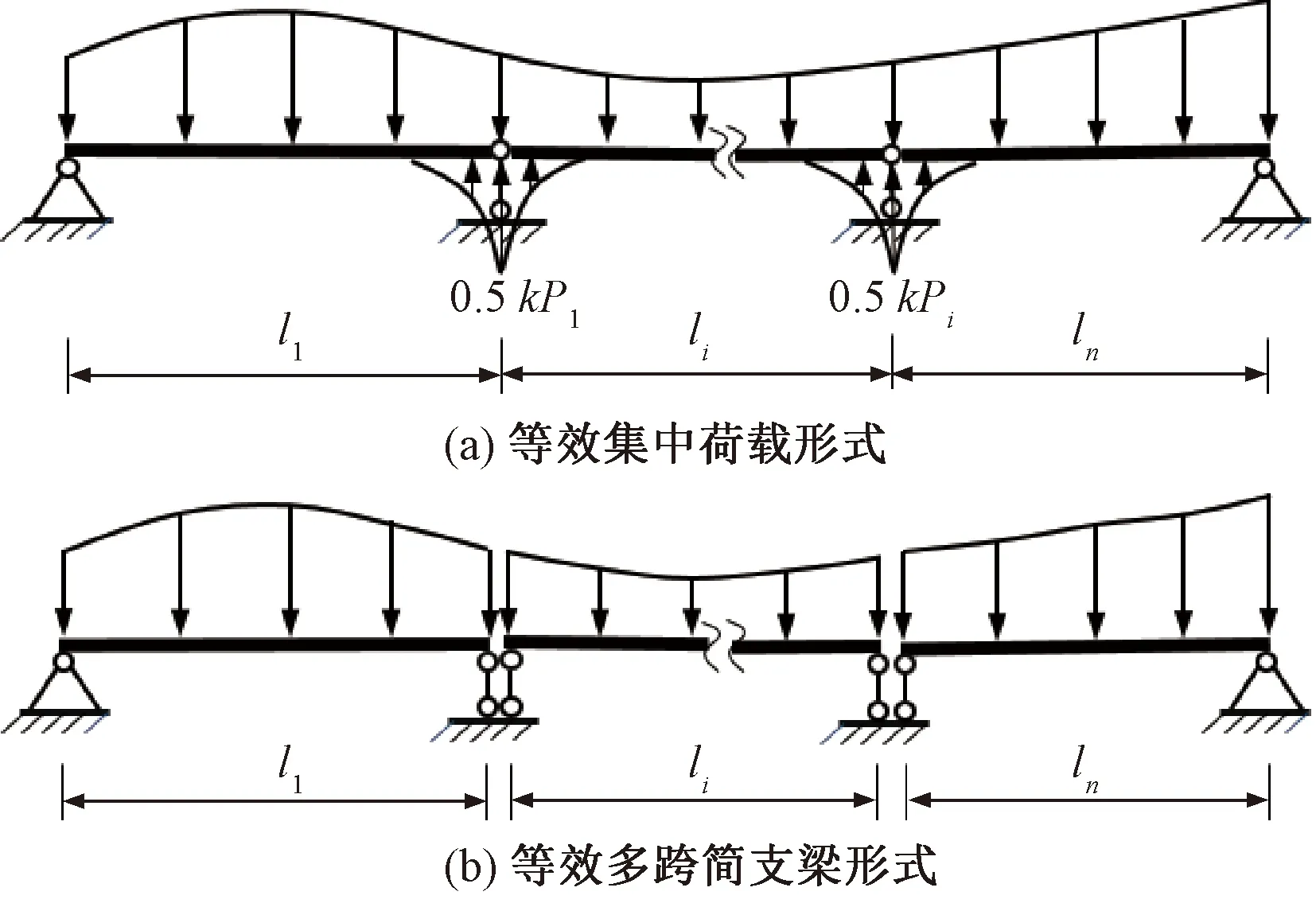
图5 连续梁的简化转换

3.3 剪切翘曲应力的修正

为验证上述简化理论的求解精度,以文献[19]承受均布荷载q的简支矩形截面梁为例进行分析。设梁厚t0=1,高度h。由式(24)～式(25)可求得的剪切挠度ws与翘曲应力为σs分别为

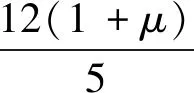
(27)

(28)

按照弹性平面梁[18]理论计算表达为

(29)

(30)

对比式(27)、式(28)与式(29)、式(30)可知,按本文简化方法计算所得的剪切挠度与弹性理论解相比为24(1+μ)/(24+15μ)。实际工程中由于泊松比μ在0.1～0.3之间,对于剪切挠度的差异在1.03～1.09之间,其差异可以忽略。剪切翘曲应力式(28)与式(30)相比,则多1+μ的系数。该对比结果与文献[20]的研究结论相同,即如果板条承受沿边缘线的拉力时,泊松比对弯曲应力无影响,如该矩形平面梁,若板条受到边缘之间拉伸荷载作用时,需考虑泊松比影响,如工字梁、箱梁的翼板承受腹板传递的剪力。因此,翼板的剪切翘曲应力需进一步修正。

由文献[20]的研究成果,当水平板条承受板纵向的线性拉伸(压缩)荷载qz时,见图6,板条的纵向修正翘曲应力σc与未修正翘曲应力σu分别为

刺史吕某……致祭于苏升、陈寅、李宽、秦陈甫、鲁余之灵。尔等五人感余诚信，力输公税，争赴先期。溪山阻深，淫潦暴至，不忍欺我，忘其险艰。[6]6372

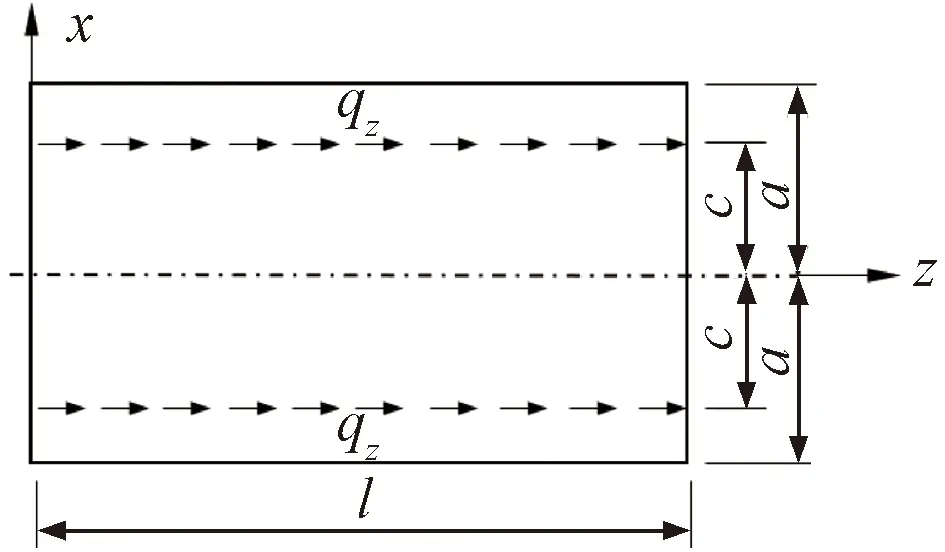
图6 矩形板条受线性拉伸荷载

σc(χ,z)=-(2+μ)[1-3(1-φ)2-3χ2-

(31)

σu(χ,z)=-(2+μ)[1-3(1-φ)2-3χ2|+

(32)

式中:φ=c/a,a为翼板宽,c为剪力作用点;χ=x/a;ξ为平面板的截面的常数;“∣”表示选择,当0≤x≤c(-c≤x≤0)时,竖线后面不考虑,当c≤x≤a(-a≤x≤-c)时,则竖线取消;对于薄壁梁的翼板,qz即相当于截面腹板传递给翼板的剪力。

利用该平面板条的翘曲应力式(31)和式(32)的应力差比来对本文所得的翘曲应力进行修正。定义翘曲应力的修正系数为ψ,其表示用修正的翘曲应力式(31)计算翼板的板宽范围翘曲应力差与用式(32)计算的翘曲应力差之比。

对图1(b)所示截面,荷载作用点为c=0,即φ=0。分别用式(31)与式(32)计算翼板χ=0与χ=1处的翘曲应力之差分别为Δσc与Δσu,则ψ为

(33)

若用Δσs表示按式(24)计算的翼板在χ=0与χ=1处应力差,如图7点划线,则实际应力差Δσc=ψΔσs。

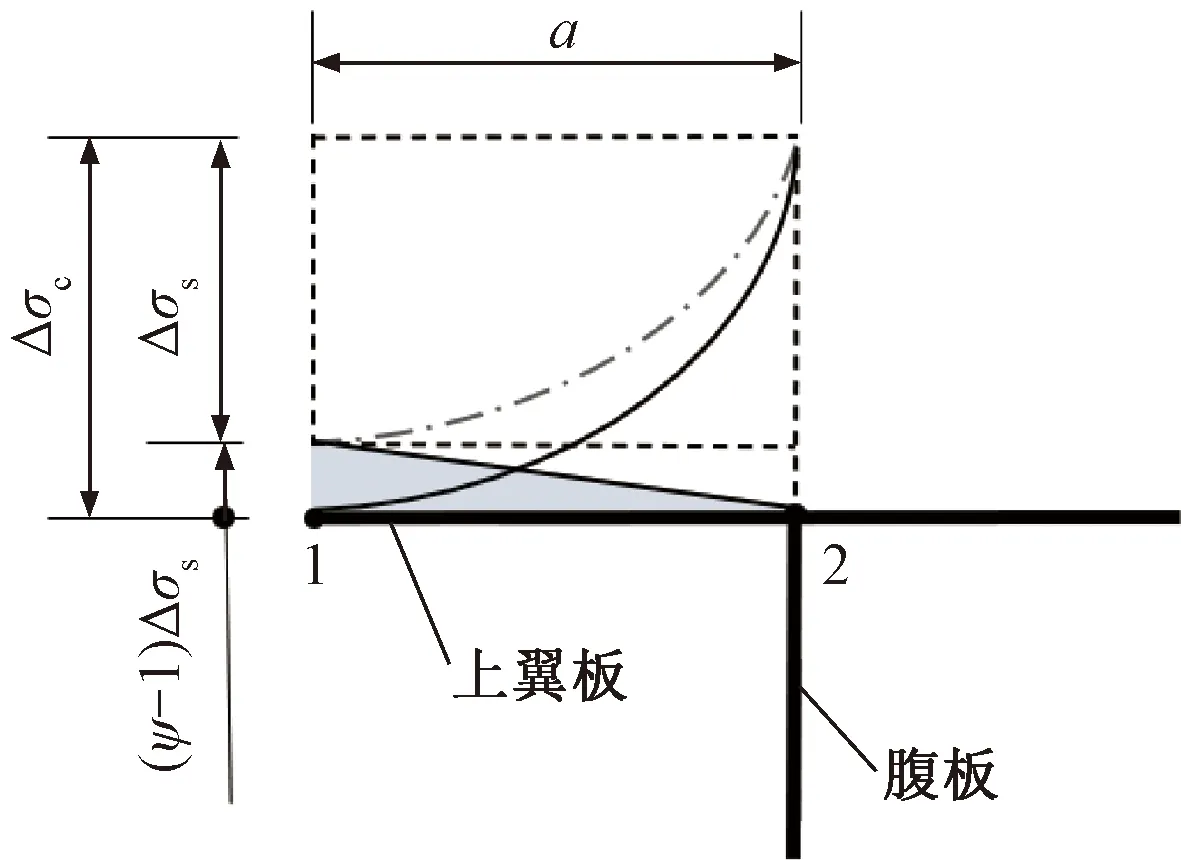
图7 剪切翘曲应力的修正

同样,对于荷载作用于闭口箱梁腹板(φ=1)时,翼板的修正系数ψ值为

(34)

对于带悬臂板的箱梁截面,闭口顶、底板的修正系数与式(34)相同,而开口悬臂板的修正系数ψ值为

(35)

4 数值算例

4.1 剪切翘曲应力修正系数分析

为验证本文提出翘曲应力修正方法的正确性,以文献[4,11-12]中带悬臂板的箱梁算例为对象,进行分析。根据文献算例给出的φ和μ值,分别计算顶板、悬臂板的应力差值比系数ψ1和ψ2。利用ψ1和ψ2计算两板的应力差值比η。作为对比,基于文献[4,11-12]的空间有限元应力结果,计算悬臂板与顶板的应力差值比ηFEM,计算结果见表1。表1中,η0为未修正翘曲应力的差值比,η0=(1-φ)2/φ2;η=η0(ψ2/ψ1)。

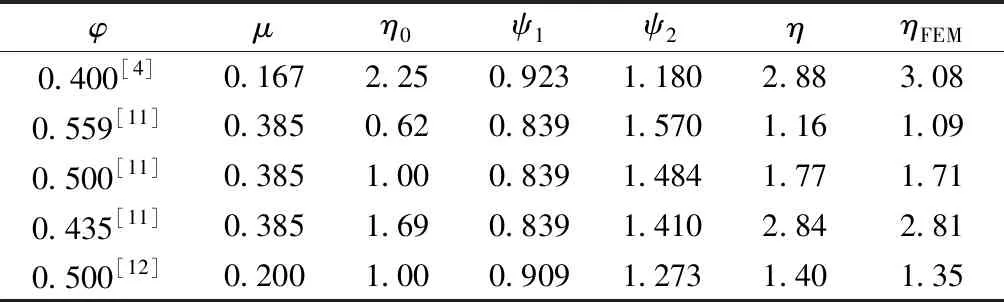
表1 应力差值系数及差值比分析

对比表1中不同板宽比和不同材料泊松比下,η与ηFEM的分析结果可知,本文方法获得应力差值比与空间有限元结果吻合较好,可说明式(33)～式(35)计算的应力修正系数ψ可靠性较强。对比未修的翘曲应力差值比η0与ηFEM可知,两者差异较大。通过表1的分析,并结合式(33)～式(35)可知,翘曲应力修正系数与板宽比φ和材料泊松比μ均有关。

4.2 简支梁挠曲分析

以图1所示的简支工字型截面梁为例进行分析。设截面的上、翼板宽a=b=100 mm,厚度均为6 mm;腹板高h=200 mm,厚度为16 mm;梁的跨度l=800 mm,材料的弹性模量为3 000 MPa,泊松比μ分别设为0、0.2和0.385。均布荷载作用于全梁腹板顶部,荷载值为p=10 N/mm。

作为对比验证,选用Ansys中的Shell63壳单元建立该简支梁的空间有限元模型(3D FEM)。全桥以四边长为10 mm的单元进行划分,共划分为4 800个单元和4 941个节点。采用简化方法及3D FEM分别计算材料泊松比为0、0.2、0.385时,跨中截面上半翼板的挠曲应力结果见表2。为减小荷载作用处应力集中的影响,表1中FEM结果为截面上、下翼板应力的平均值。

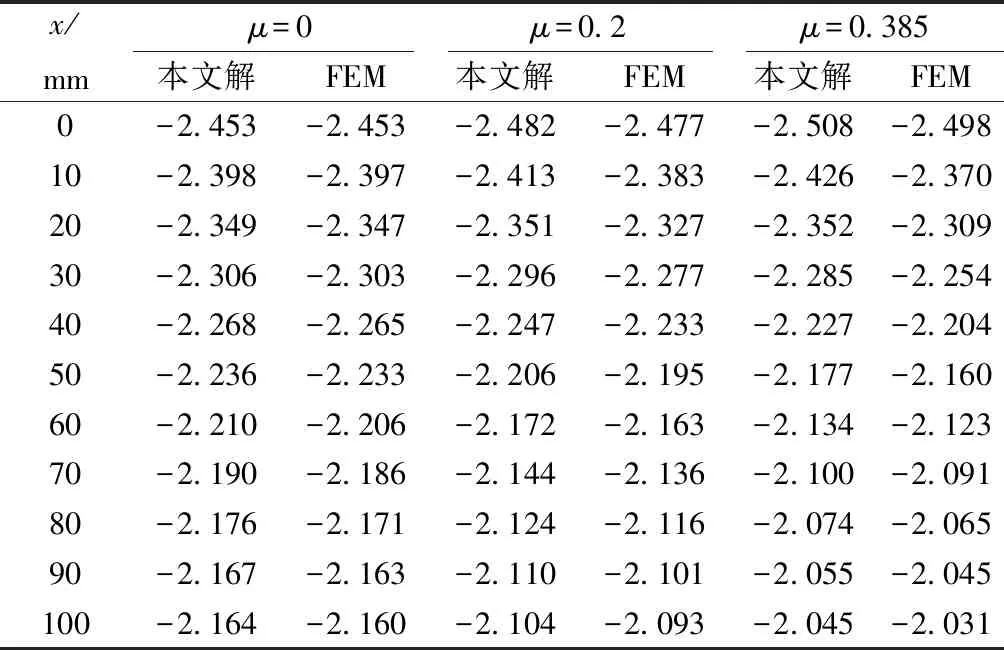
表2 上半翼板的挠曲应力 MPa

对比表2中不同材料泊松比所对应的挠曲应力可知:材料泊松比μ对翼板的挠曲应力结果有一定影响;材料泊松比μ对翼板的挠曲应力差有影响。因此,在求解薄壁梁翼板应力时需考虑泊松比影响。对比不同材料泊松比下本文方法所得应力与FEM结果可知,当μ=0时,两者应力最大误差为2.3‰;当μ=0.2时,两者应力最大误差为1.2%;当μ=0.385时,两者应力最大误差为2.3%。通过上述分析可得采用本文简化方法可得到较为精确的挠曲应力。

为验证简化分析方法对挠度计算的适用性,分别按初等梁理论、简化方法及3D FEM计算简支薄壁梁的挠度曲线见图8。

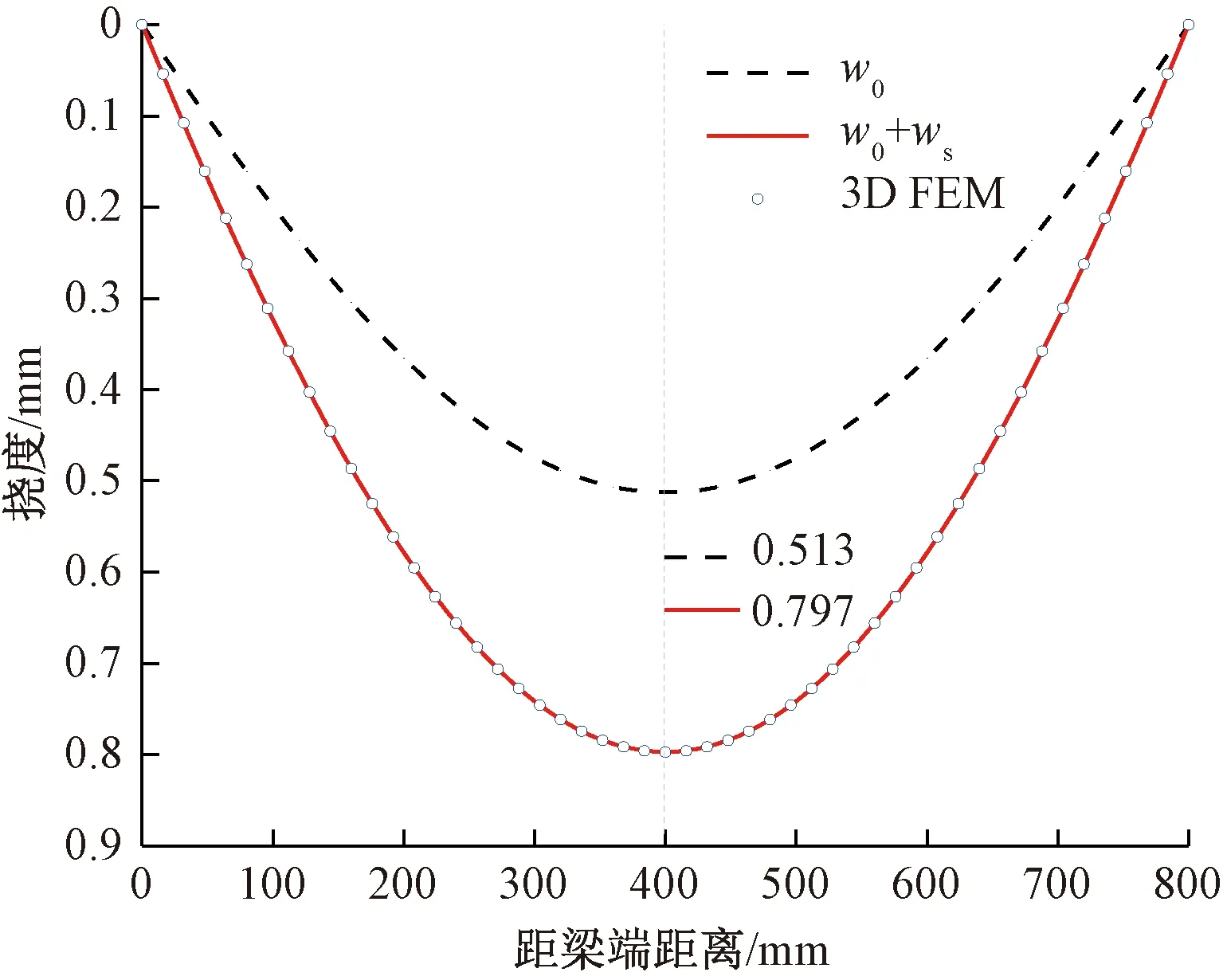
图8 荷载作用下的挠度曲线

对比观察图8可知,按照简化方式计算的挠度值与3D FEM结果吻合良好,说明本文方法求解挠度精度较高。在均布荷载作用下,剪切挠度为初等梁挠度的0.55倍,可见剪切变形对薄壁梁的挠度影响较大。

4.3 连续梁的挠曲分析

为验证本文提出的连续梁简化分析方法的有效性,选取4.2节中截面尺寸,连续梁的跨径组合为(1 000+1 200+1 000)mm。材料参数和4.2节相同,泊松比设为0.385。承受的荷载工况为:均布荷载p=10 N/mm;边跨、中跨的跨中部均承受集中荷载P=5 kN。按照3.2节所述的简化方法求解连续梁在工况1、2荷载下中支点的剪切支反力值P1和P2。同时,采用变分法[14]求解剪切支反力,并将上述方法求得的剪切支反力见表3。表3中,差值比=(简化计算值-精确值)/精确值。

表3 中支点的剪切支反力

由表3差值比结果可知,按照简化分析方式求得剪切支反力与精确值相差在3%以内。显然,按照简化方式可以满足工程要求。

为验证简化分析方式求解连续梁应力的准确性,不同荷载下简化分析方法与空间有限元(3D FEM)方式求得的腹板顶点应力纵向分布结果见图9。

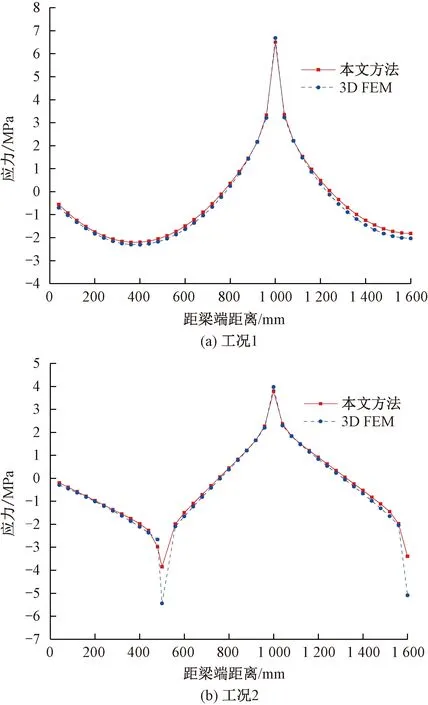
图9 不同荷载条件下腹板顶点应力沿梁轴的分布图

由图9可知,除去图9(b)中集中荷载作用处截面,其余各截面采用本文简化方法求得的应力与3D FEM结果吻合良好。集中荷载处截面的差异是因应力集中导致。通过对比分析结果可说明简化方式求得连续梁的应力具有足够精度。

表4分别给出了采用本文简化方法、精确方法[14]与3D FEM方式计算的连续梁边跨和中跨跨中截面的挠度结果。表4中,wJs与ws分别为精确解与简化方法所得的剪切挠度,差值比=(wJs-ws)/(3D FEM)。

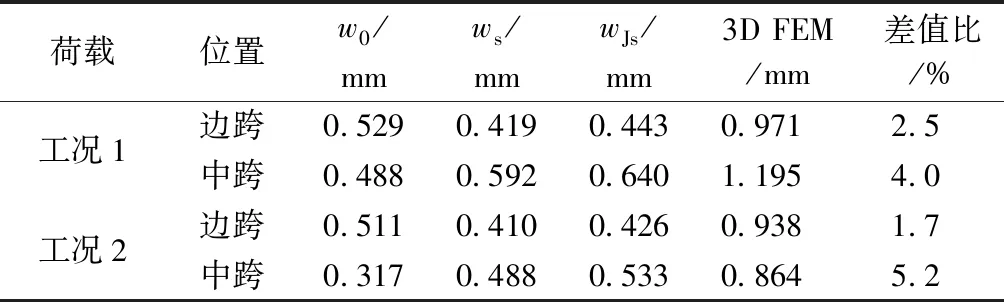
表4 跨中挠度对比

由表4的对比分析可知,按照两种方法计算的薄壁梁跨中挠度与3D FEM的计算结果均吻合良好,采用本文简化方式与精确方法计算的挠度相差均在6%以内,说明简化方法精度满足工程要求;工况1荷载下,边跨剪切挠度约为初等梁挠度的0.84倍,中跨约为1.31倍;工况2荷载下,边跨剪切挠度约为初等梁挠度的0.83倍,中跨约为1.68倍;对比简支梁结果可知,剪切变形对连续梁的影响更为重要。

5 结论

1)从薄壁梁各壁板的剪切应变与位移的关系出发,导出考虑剪切变形影响的挠曲位移函数。选取剪切变形引起的挠度为独立位移,通过解耦挠曲性能获得了剪切挠度与翘曲应力的简化公式。

2)基于平面板条的应力分析结果,导出薄壁梁翼板翘曲应力的修正计算式。利用中支点变形连续条件,给出连续梁的剪切挠曲简化分析方法。

3)与传统分析方法相比,本文方法求解过程简便,且对连续梁的适用性较强,便于在实际工程应用。

4)数值算例表明,本文方法求得的应力结果与3D FEM结果最大误差在3%以内,挠最大误差为6%以内,说明本文方法可靠且精度较高;材料的泊松比及板宽比对薄壁梁翼板的翘曲应力影响较大。