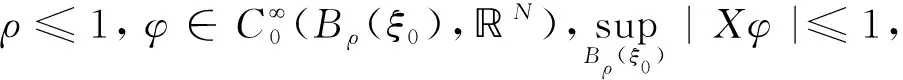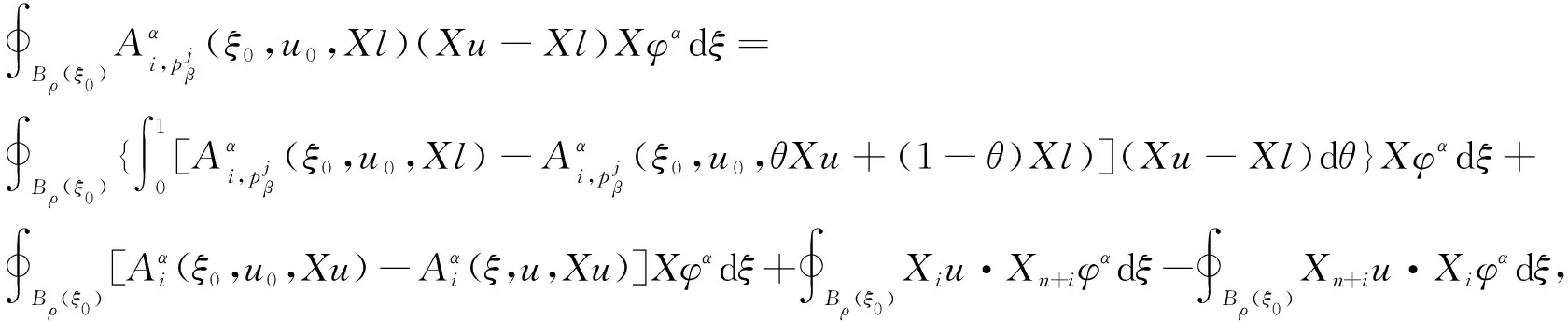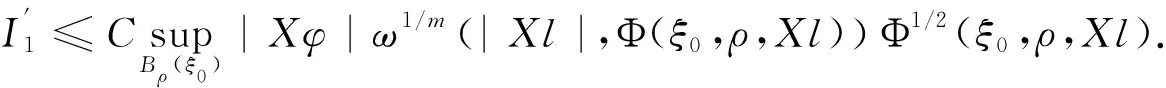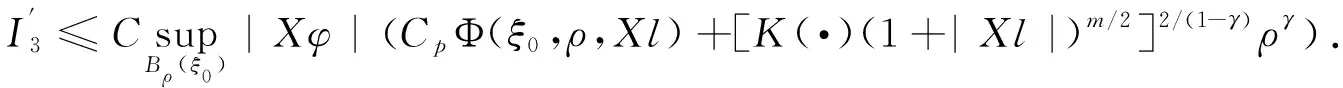Heisenberg群上带漂移项的次椭圆方程组弱解的正则性*
段国强,廖冬妮,朱 彦
(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)
0 引言和主要结果
本文研究Heisenberg群上带漂移项的齐次次椭圆方程组,形如

(1)
其中Ω⊂Hn=2n+1为有界区域,
近年来,次椭圆方程(组)弱解的正则性研究得到广泛关注, 并取得丰富成果,详见文献[1-9].众所周知,带漂移项算子具有重要的理论和应用意义,这类算子通常出现在物理学、自然科学和统计模型等传输扩散方程中.最近,ZHANG和NIU在文献[10]中研究了Heisenberg群上一类带漂移项的拟线性次椭圆方程,并建立弱解的C1,α正则性,进一步地,ZHANG和WANG在文献[11]中考虑了带漂移项的具有VMO系数的次椭圆方程组,证明了弱解的C0,α部分连续性.然而,当系数为Hölder连续时,Heisenberg群上带漂移项的次椭圆方程组,其弱解的C1,α正则性如何建立?
本文将应用Heisenberg群上的A-调和逼近技巧,克服带漂移项没有先验假设和方程组书非线性的困难,得到弱解的最优C1,α连续性.






(2)
其中K(·)∶[0,∞)→[0,∞)是单调递增的.不失一般性,取K(·)≥1.
由(H1)知:存在一个连续的非负有界函数ω(s,t)∶[0,∞)×[0,∞)→[0,∞)使得

(3)
其中ω(s,0)=0,并且对于固定的t,ω(s,t)对s是单调递增的;对于固定的s,ω(s,t)对t是凹的且单调递增的.
由(H2)得

(4)
其中λ′为正常数.
本文的主要结果如下:
定理1在结构条件(H1)-(H3)假设下,设u∈HW1,m(Ω,N)是方程组(1)的弱解,即

则存在一个开子集Ω0⊂Ω,有u∈Γ1,γ(Ω0,N),γ与(2)式一致.此外,Haarmeas(ΩΩ0)=0,ΩΩ0⊂Σ1∪Σ2,其中

1 Heisenberg群基础知识
Heisenberg群Hn=2n+1定义群乘法为:其中
零元素为0,并且(ξ1,t)的逆元为(-ξ1,-t),其相应Lie代数的一组基向量场为:

(5)
关于Lie括号满足:[Xi,Xn+i]=-[Xn+i,Xi]=T,[Xi,Xj]=0和[T,T]=[T,Xi]=0.
相应于欧氏空间经典的Hölder空间,下面给出Heisenberg群上Folland-Stein空间定义.

为Folland-Stein空间.
定义2设Ω⊂Hn,1≤m<∞,μ≥0,记
m,μ(Ω)={u∈L∞<∞}.
引理1令ξ∈Ω⊂Hn,m>1和Q<μ≤Q+m,则m,μ(Bρ(ξ))⊂Γγ(Bρ(ξ)),γ=(μ-Q)/m.
下面,引进Heisenberg群上的A-调和逼近引理6和常系数次椭圆方程组弱解的先验估计.
引理2设λ和L为固定的正数,和n,N∈,其中n≥2,若对任意的ε>0,存在δ=δ(n,N,λ,ε)∈(0,1],有:
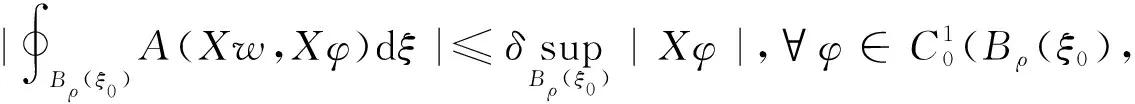
则存在一个A-调和函数h,使得∮Bρ(ξ0)|Xh|2dξ≤1和ρ-2∮Bρ(ξ0)|h-w|2dξ≤ε.
引理3设u∈HW1,m(Bρ(ξ0),N)是定义在Bρ(ξ0)上的A-调和函数,则存在C0≥1使得
2 Caccioppoli型不等式
本节重点建立方程组(1)满足的Caccioppoli不等式.
引理4设u∈HW1,m(Ω,N)是方程组(1)在条件(H1-H3)下的弱解,则对任意的N,Xl∈2n×N,和任意的ρ∶0<2ρ ∮Bρ(ξ0)[|Xu-Xl|2+|Xu-Xl|m]dξ≤C(ρ-2∮B2ρ(ξ0)|u-l|2dξ+ ρ-m∮B2ρ(ξ0)|u-l|mdξ+[K(|u0|+|Xl|)+(1+|Xl|m/2)]2/(1-γ)(2ρ)2γ), ∮B2ρ(ξ0)Xiu·Xn+i(φ2(u-l))dξ-∮B2ρ(ξ0)Xn+iu·Xi(φ2(u-l))dξ. 由φ=φ2(u-l)可得 (6) 将以上式子相加,并利用(2)可得 (7) 应用(4),则(7)的左侧可估计为 下面,分别估计(7)中右端五项. 对任意小的正数ε,应用Young不等式和|Xφ|≤Cρ-1,有 I1≤Cε∮B2ρ(ξ0)|φ|2|Xu-Xl|2dξ+Cε-1ρ-2∮B2ρ(ξ0)|u-l|2dξ+ Cε∮B2ρ(ξ0)|Xu-Xl|m|φ|m/(m-1)dξ+Cε1-mρ-m∮B2ρ(ξ0)|u-l|mdξ. (8) 注意到(2ρ/ρ)2γ≥1,和(2ρ)2γ/(1-γ)≤(2ρ)2γ,可得 I2≤ε∮B2ρ(ξ0)φ2|Xu-Xl|2dξ+ε-1ρ-2∮B2ρ(ξ0)|u-l|2dξ+ε-1[K(·)(1+|Xl|)m/2]2/(1-γ)(2ρ)2γ. (9) 类似地,I3和I4可估计为 I3≤4Cρ-2∮B2ρ(ξ0)|u-l|2dξ+[K(·)(1+|Xl|)m/2]2/(1-γ)(2ρ)2γ. (10) 和 (11) 最后处理I5,注意到l不依赖于t,那么Tl=0,即XiXn+il-Xn+iXil=0,那么利用|Tφ|≤c1ρ-2得 I5≤c1ρ-2∮B2ρ(ξ0)|u-l|2dξ. (12) 将(8)-(12)代入(7)中,不难得到 Cε1-mρ-m∮B2ρ(ξ0)|u-l|mdξ+(2ε-1+5)[K(·)(1+|Xl|)m/2]2/(1-γ)(2ρ)2γ. 下面将给出定理1的证明,主要分为三步:第一步是建立线性化工具(引理5),它是应用A-调和逼近引理研究非线性次椭圆方程组弱解正则性的桥梁;第二步是应用逼近引理和线性化工具建立过剩泛函的改进估计;最后一步是建立过剩泛函改进估计的迭代形式,并利用Campanator空间关于Hölder连续性的刻画得到正则性结果. Φ1/2(ξ0,ρ,Xl)+Φ1/2(ξ0,ρ,Xl)+Φ(ξ0,ρ,Xl)+ργH(|u0|+|Xl|)], 其中C1=C1(m,Q,a,b)>1,H(τ)=[K(τ)(1+τ)m/2]2/(1-γ). 证明注意到 在球Bρ(ξ0)上利用(6)和弱解的定义,可得 (13) 由(H1)可得 (14) 将(14)代入(13)有 (15) 应用Hölder不等式,t→ω2(s,t)的凹性质,Jensen不等式和m/(m-2)≤2可得 (16) 由(H3),Young不等式,K≤K2,ρ2γ≤ρ和2γ≤m/2+γ≤m/(1-γ)可得 (17) 利用Young不等式,Poincaré不等式和ρ2γ/(1-γ),ρ2γ/(2-γ)≤ργ有 (18) (19) 将(16)-(19)代入(15),即可得到结论. 类似于文献[4]的步骤,可建立过剩泛函改进估计和迭代估计,证明过程不再赘述. 引理6设γ∈(0,1),θ∈(0,1),若存在正数C2,C3和引理2的δ,使得小条件 (20) (21) 和 2C2ργH(1+|uξ0,ρ|+|(Xu)ξ0,ρ|)≤δ/2. (22) 成立,则 其中Φ(ξ0,ρ)=Φ(ξ0,ρ,(Xu)ξ0,ρ),H0=H(1+M1). 引理7对任意的n∈,|uξ0,θnρ|+|(Xu)ξ0,θnρ| 至此,应用标准化过程即可得到弱解u∈Γ1,γ(Ω0,N).详细证明过程可参见文献[1].


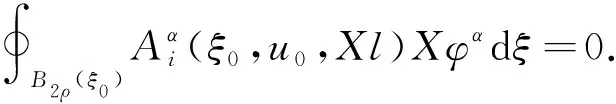

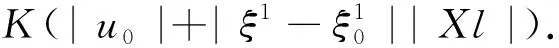
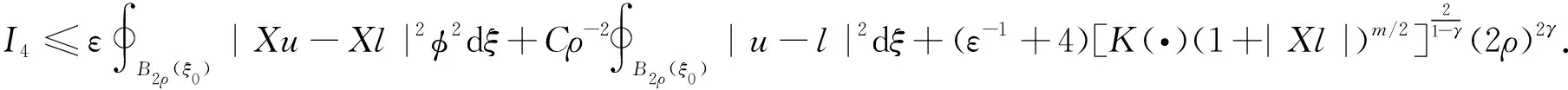

3 定理1的证明