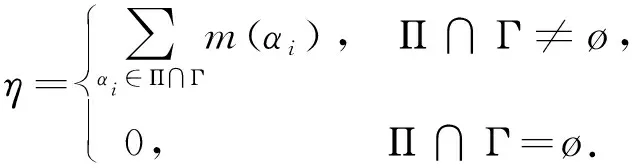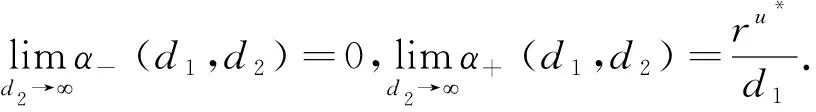一类扩散捕食食饵模型的非常数正稳态解*
高建平,张江洪,练文燕
(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)
0 引言
种群生态学中,两种群间的相互作用关系存在多种形式,其中,捕食关系是一种常见而又基本的种群关系.继Lotka和Volterra的两个开创性工作[1-2]之后,越来越多的生物数学家通过建立微分方程模型来研究捕食关系[3-5].基于假设捕食者以logistic形式增长并且其环境容纳量与食饵的种群数量成正比,给出如下捕食模型的一般形式:

(1)
其中,u和v分别代表食饵,捕食者的种群密度;r表示捕食者的增长率;1/l表示捕食者捕食食饵的转化率;p(u,v)是功能型反应函数,它刻画了捕食者捕食食饵的能力.方程(1)中的捕食者方程是第一次由Leslie和Gower在1960年提出的[6].因此,捕食系统(1)也被称为Leslie-Gower型捕食食饵模型.针对不同形式下的功能型反应函数p(u,v),有不少研究者给出了模型(1)的动力学行为研究[7-10].
在模型(1)中考虑捕食者和食饵在空间区域内随机游走,便可得到如下反应扩散的捕食食饵系统
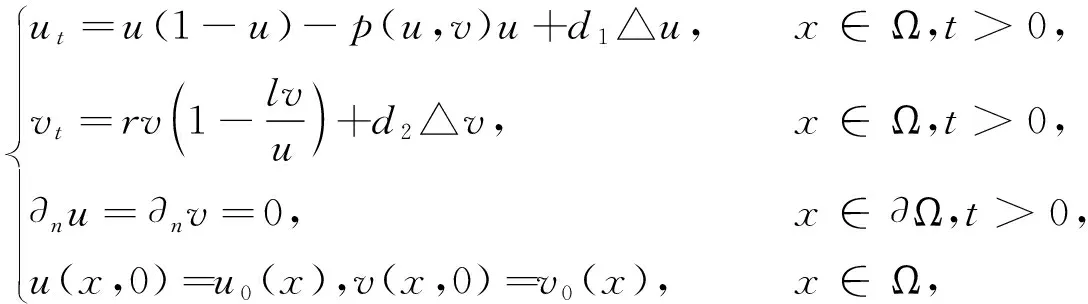
(2)
其中,d1和d2分别代表食饵和捕食者的自扩散系数;Ω是有界光滑区域;n表示边界∂Ω的单位外法向量.在这里,采用了齐次Neumann边界条件,即在区域边界∂Ω上没有种群的进出.Shi[11-12]等给出了带有Ratio-Depenent功能反应和Crowley-Martin功能反应函数的扩散捕食模型(2)的时空斑图动力学研究.Sun[13]等在(2)中考虑Beddington-DeAngelis功能反应函数,给出(2)稳定性及Turing不稳定性研究.对(2)还存在更多的研究工作[14-16].
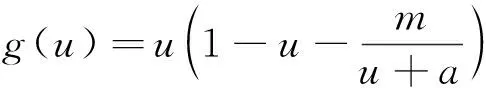
基于此,令l=1,本文在(2)加入组分Allee效应并且考虑Beddington-DeAngelis功能反应函数,得到

(3)
这里本文假设0 a0u3+a1u2+a2u+a3=0, (4) 其中,a3=m-a,a2=a+mb+mc+aμ-ab-ac-1,a1=b(a-1)+c(a-1)+μ+1,a0=b+c.注意到a0>0和a3<0,于是,当下述条件成立时,方程(4)具有唯一的正根: (5) 因此,当条件(5)满足时,模型(3)具有唯一的内部正常数平衡点E1=(u*,u*). (6) 定理1E0总是不稳定的; 证明这里只给出的证明.注意到由条件ru* 与模型(3)对应的稳态解方程为 (7) 要研究模型(3)的非常数稳态解等价于研究椭圆系统(7)的非常数正解. 给出(7)的任意正解的上下界估计.首先,运用极值原理[26],得到下面这个上界估计结果. 于是 (8) (9) 下面给出大扩散系数下系统(7)非常数正解的不存在性结果. 定理2存在一个正常数d*=d*(m,a,b,c,r),使得当min{d1,d2}>d*时,(7)不存在非常数稳态解. (10) (11) 在条件(5)成立的情形下,本小节将利用Leray-Schauder度理论讨论扩散系数变动时模型(3)的非常数正稳态解的存在性,即研究系统(7)的非常数正解的存在性.记 将(7)写成 (12) (d1r-d2ru*)2>-4d1d2r(ru*+σ), (13) 成立时,g(d1,d2;α)=0具有两个不同的实根α-(d1,d2),α+(d1,d2)且满足α-(d1,d2)<α+(d1,d2),其中 记Π=Π(d1,d2)={α∶α≥0,α∈(α-(d1,d2),α+(d1,d2))},Γ={α0,α1,α2,…}.令m(αi)是特征值αi的重数,根据文献[28],可以得到以下引理: α+(d1,d2)∈(αj,αj+1),α- (14) α-(d1,d2)<α+(d1,d2)<α1. (15) (16) 一方面,对W∈∂Λ,有H(W;t)≠0对所有t∈[0,1]都成立.于是根据Leray-Schauder度的同伦不变性[28]可知, deg(H(W;0),Λ,0)=deg(H(W;1),Λ,0). (17) 证明这里证明与定理3类似,这里略去.1 常数平衡点的稳定性
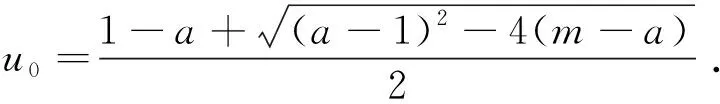
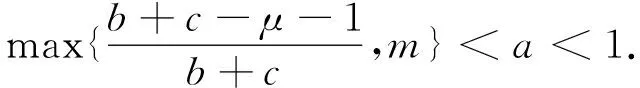




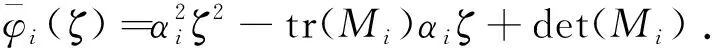
2 非常数正稳态解的存在性与不存在性
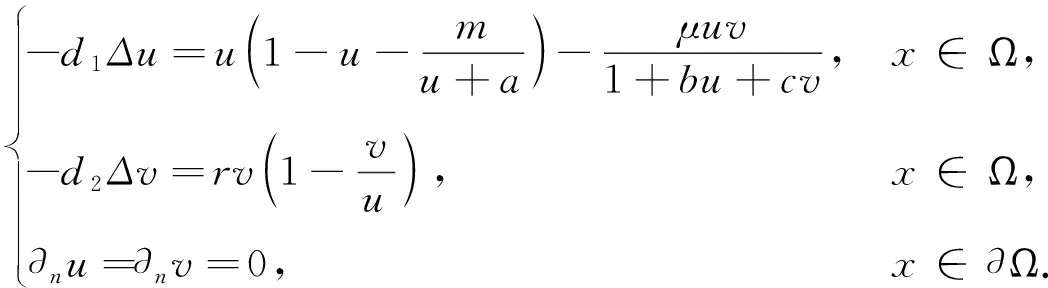
2.1 先验估计
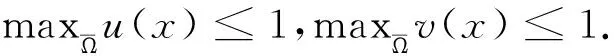


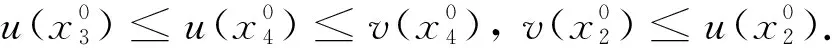

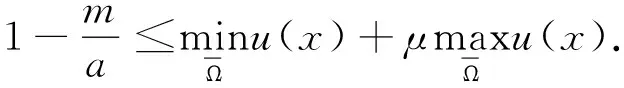
2.2 非常数稳态解的不存在性

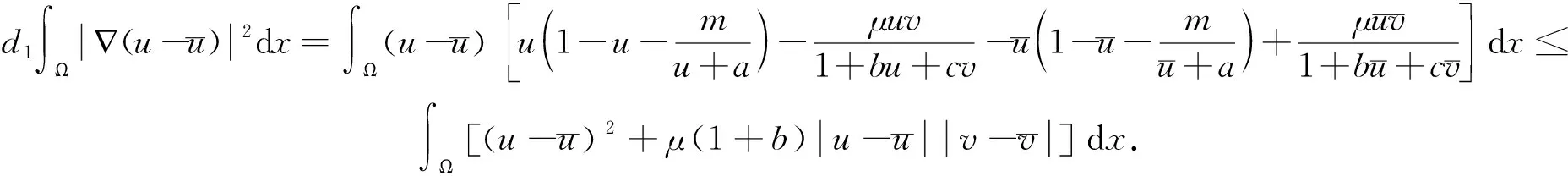



2.3 非常数稳态解的存在性