一种新开发的ANCF缆索单元

郑茂盛, 陈建平, 童明波

(南京航空航天大学航空学院, 南京 210016)

线缆是一类具备大挠度变形特征的柔性结构,可用于控制安装、设备连接、电力传输、光信号传输等。由于重量轻、阻尼小、抗拉强度高、柔性好等特点使其在工程实践中被广泛应用[1-2]。在现代工艺中几乎可以制造出满足各类工程需要的线缆。与此同时,复杂的层级结构、多样的绳股缠绕方式、不同的层间材料属性都极大地影响着线缆的动力学行为。就系绳操作的水下系统而言,系留线缆所带来的不必要的阻力和非线性内力很大程度上影响着水下机器人运动。而对于空中系浮系统而言,无论是在升空阶段、系泊阶段还是回收阶段,系留线缆始终起到承力的关键作用[3]。因此,对于该类缆索结构的动力学分析至关重要,精确有效的建模方案也引起了很多研究人员的关注。

多层圆形截面的缆索在材料属性和几何变形中都表现出了典型的非线性特征。对于这类具有几何大变形特征的柔性结构进行动力学建模主要方法有以下几种方法。

方法一是利用集中质量法对缆索进行大规模离散,相邻质点之间利用弹簧-扭簧进行连接,并取各质点在惯性空间中的直角坐标为广义坐标,利用 Lagrange 方程建立系统的运动微分方程,Buckham等[4]对此进行了充分的研究。这种方法简便易懂,但其求解精度较低,且当节点划分过密时,求解效率将大大降低。

方法二是由Kamman等[5]提出的利用基于伪刚体理论的有限段离散化方法进行动力学建模,但该方法的缺点同样在于随着有限段数目的增加,动力学方程的求解效率会大大降低。

方法三是可以利用连续介质力学对其进行动力学建模。将缆索处理为具有大挠度变形的细长弹性梁,再利用牛顿定律或Hamilton 原理推导出运动的偏微分方程,最后利用差分格式进行离散求解。Koh等[6]对此进行了详细的叙述,但其难点在于非线性偏微分方程的数值求解。

方法四是由Shabana[7]于20世纪90年代提出的绝对节点坐标方法(absolute nodal coordinate formulation,ANCF)。其基本思想是将有限元中的单元节点用惯性坐标系中的绝对坐标进行描述,并用斜率矢量代替传统的节点转角坐标以得到系统在全局坐标系下的运动方程。该方法具有质量矩阵为常值矩阵、无科氏力和离心力等优点。其能够很好地反映出柔性缆在拉伸、扭转、弯曲等变形下的复杂动力学行为[8]。

与Gerstmayr等[9]提出的高阶ANCF梁单元不同,现利用Shen等[10]的全参数高阶ANCF梁单元的形状函数对缆索进行运动学描述。原因在于后者在抑制泊松锁定方面具有极大优势。此外,在对单元子域数值积分的研究工作中,Orzechowski[11]选用高斯积分点对圆形截面单元进行了数值分析。随后,Orzechowski等[12]又开发了一种能够分析矩形横截面的层合梁模型。此后,Lan等[13]对多层圆形截面单元子域的积分提出了合理、有效的数值策略。

针对于一些具有绝缘层的工程缆索而言,护套层通常选用橡胶、聚酯氨等材料以用于绝缘、抗磨和防腐化等。而这些材料的泊松比接近于0.5,能够表现出不可压缩和超弹性的力学特性。对于该类不可压缩材料的研究工作在文献[14]中得到概括总结,其中包括Neo-hookean模型、Mooney-Rivlin模型以及Yeoh模型[14]等。而由于应变能密度函数的展开式仅保留了有限的项数,Neo-hookean模型、Mooney-Rivlin 模型均无法准确地反映大变形状态下材料的应力-应变关系,特别是无法反映“S”形应力-应变曲线,因此其只适用于应变水平较低的情况[14]。相反,虽然Yeoh 模型[14]在预测大变形简单应变问题上具有一定优势,但其在预测等双轴拉伸问题上将会出现“偏软”的较大误差,无法精确地处理大变形复杂应变问题。

对于利用绝对节点坐标方法对上述工程缆索进行动力学建模的研究而言,近些年学者多将超弹性材料的Mooney-Rivlin模型[15-17]、Yeoh模型[14]应用到ANCF单元中。徐齐平等[18]通过引入罚函数,推导Yeoh模型[14]的弹性力矩阵,并采用绝对节点坐标方法建立大变形硅胶板的动力学方程。郭嘉辉等[19]借助平面二维ANCF梁单元分别构建了基于Neo-hookean模型、Mooney-Rivlin[15-17]模型以及Yeoh模型[14]的不可压缩超弹性橡胶梁的动力学模型。

但是对于广泛应用于浮空器系泊当中的系留缆索而言,应用ANCF方法对其精确动力学建模的相关研究较少。此外,为了进一步克服Mooney-Rivlin模型[15-17]难以准确地反映大变形状态下超弹性材料的应力-应变关系以及应变适用水平低、范围小等问题,首次将改进后的Yeoh模型[14]应用于系留缆索的动力学建模当中,并利用三维高阶ANCF梁单元来精确刻画缆索的运动及变形[20],开发一种新型的基于改进Yeoh超弹性模型的ANCF缆索单元。同时,通过比较几种应用不同超弹性本构模型的ANCF单元,对其动力学响应的特征与差异进行对比分析,为后续对于径向多层圆截面缆索的动力学建模研究提供一定的指导。

1 材料的力学特性

图1为车载式系留监测系统的示意图。针对于系留系统中的系留线缆而言,其径向层级结构由内到外依次为内导体、绝缘层、承力层、外护套。铜、铝等高导电的金属材料多用于内导体;绝缘层多选用绝缘效果不错的聚乙烯(PE)、交联聚乙烯(XLPE)以及氟塑料等;芳纶、聚对苯撑苯并二噁唑纤维(PBO)等新型高强度材料往往作为抗拉件应用于承力层;橡胶、热可塑性聚氨酯(TPU)材料则应用于护套层当中[3]。线缆的横截面如图2所示。

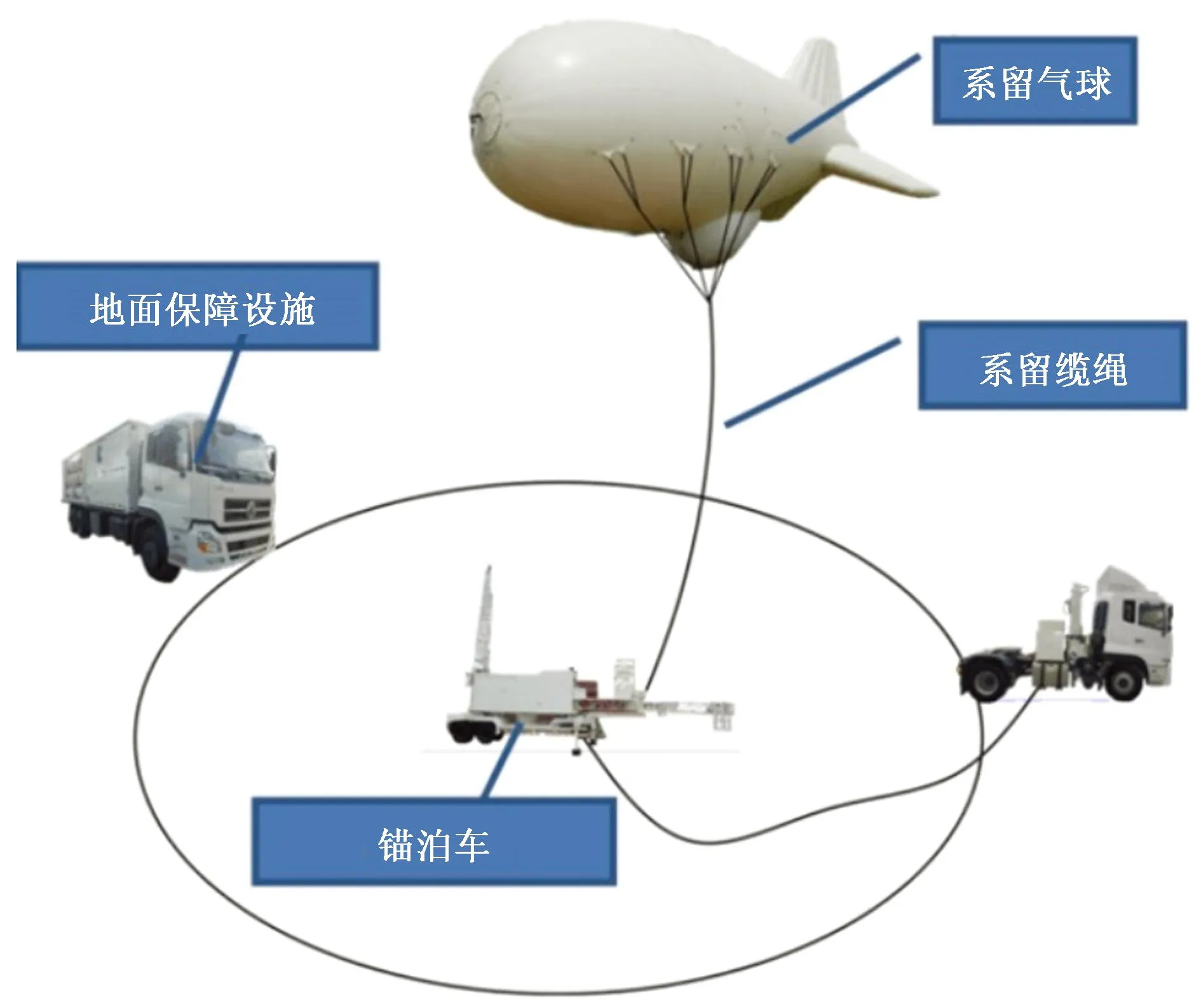
图1 车载式系留检测系统

图2 线缆的横截面

1.1 黏弹性材料的Kelvin-Voigt模型

García-Vallejo等[16]基于瑞利函数提出ANCF单元的内部阻尼模型。其在考虑泊松效应的同时可以很好地解释多轴应力状态下的线性黏弹性关系。对于均匀各向同性黏弹性材料而言,其本构方程的表达式为

(1)

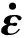
(2)

D=

(3)

对黏弹性材料而言,有

(4)

体积模量K可表示为

(5)

式中：λ和μ分别为第一拉梅常数和第二拉梅常数;E为杨氏模量;v为泊松比;γd和γs分别为偏应力耗散因子和膨胀应力耗散因子。

1.2 改进后的Yeoh模型

引入右Cauchy-Green变形张量C=FTF,其中F为变形梯度。于是得到右Cauchy-Green变形张量的3个不变量I1、I2、I3,可分别表示为

(6)

式(6)中：tr为矩阵的迹。

可以将改进后的Yeoh模型[14]中的应变能密度函数写为

Wp=C10(IC-3)+C20(IC-3)2+
C30(IC-3)3+C01(IIC-3)

(7)

式(7)中：IC和IIC分别为变形张量C的第一、第二不变量;C10、C20、C30、C01为4个模型常数。

第二Piola-Kirchhoff张量可表示为

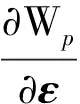
(8)

式(8)中：ε为Green-Lagrange应变张量。

2 动力学建模

2.1 运动学分析

图3为三维全参数高阶ANCF梁单元的示意图。

ri为节点i处的位置矢量;ri,x,ri,y,ri,z为节点i处的3个梯度矢量;ri,yz,ri,yy,ri,zz在几何上解释为曲率矢量,其对泊松锁定的抑制具有关键作用

利用如式(9)所示的多项式来近似表示单元任意点于惯性坐标系下的位移。

r=[a0+a1x+a2y+a3z+a4xy+a5xz+a6x2+a7x3+a8yz+a9y2+a10z2+a11xyz+a12xy2+a13xz2b0+b1x+b2y+b3z+b4xy+b5xz+b6x2+b7x3+b8yz+b9y2+b10z2+b11xyz+b12xy2+b13xz2c0+c1x+c2y+c3z+c4xy+c5xz+c6x2+c7x3+c8yz+c9y2+c10z2+c11xyz+c12xy2+c13xz2]

(9)

此时利用节点的全局位置矢量、3个方向的梯度矢量以及曲率矢量作为单元的广义坐标,可将式(9)变换为

(10)

式(10)中：I为单位矩阵;q为单元的广义坐标列阵。

s1=1-3ξ2+2ξ3

s2=l(ξ-2ξ2+ξ3)

s3=lη(1-ξ)

s4=lζ(1-ξ)

s5=l2ηζ(1-ξ)

s8=3ξ2-2ξ3

s9=l(-ξ2+ξ3)

s10=lξη

s11=lξζ

s12=l2ξηζ

(11)

单元内任意点的速度与加速度坐标列阵同样可表示为

(12)

2.2 动力学分析

2.2.1 惯性力的虚功

基于2.1节中对ANCF单元运动学的分析,其惯性力的虚功可表示为

(13)

式(13)中：ρ1、ρ2分别为内、外层的材料密度;A1、A2分别为内、外层的截面面积;VI、VII分别为内、外层的体积积分域。

结合式(10)、式(12),可将式(13)变换为

(14)

式(14)中：δW1为惯性力的虚功;M为缆索单元的质量矩阵,是一个42×42阶的对称正定常值矩阵;δq为广义坐标的变分。

2.2.2 黏弹性力的虚功

基于连续介质力学的相关理论,6个应变分量于全局坐标系下分量值可写为

(15)

式(15)中：rx、ry、rz为位置矢量r相对于x、y、z坐标方向的3个梯度矢量。

基于1.1节中对黏弹性材料本构关系的分析,此时黏弹性力的虚功可表示为

δW2=-δqTQLayerI

(16)

式(16)中：δW2为黏弹性力的虚功;QLayerI为广义非线性黏弹性力列阵,可以记为

(17)

式(17)中：K为42×1阶的广义弹性力列阵,其具备高度的非线性特征;C为42×42阶的广义阻尼系数矩阵。

K与C也可以记为

(18)

2.2.3 不可压缩材料弹性力的虚功

基于1.2节中对护套层力学性能的基本分析,可以得到护套层非线性弹性力的虚功表达式为

δW3=-δqTQLayerII

(19)

式(19)中：δW3为护套层弹性力的虚功;QLayerII为其非线性弹性力列阵,QLayerII的表达式为

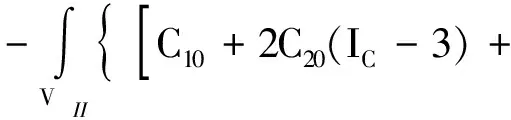
(20)

而改进后的Yeoh模型常数取文献[14]中的拟合结果为：C10=1.7×105Pa,C20=-1.55×103Pa,C30=46.1 Pa,C01=5.24×103Pa。

2.2.4 外力的虚功

若缆索的内、外层单元分别受到均布体力f1、f2和作用于a位置的集中力p影响时,其由外力项所引起的虚功可表示为

(21)

式(21)中：ra为a位置于全局坐标系下的位置矢量;δW4为外力的虚功。将式(21)可简化为

δW4=δqTQ

(22)

Q为单元的广义外力列阵,可表示为

(23)

式(23)中：Sa为位置a处的形函数矩阵S。

2.2.5 动力学方程

基于虚功原理,综合上述对相关虚功的具体分析,建立ANCF缆索单元的动力学方程。

根据虚功原理有

δW1+δW2+δW3+δW4=0

(24)

由于广义坐标变分的独立性,将式(14)、式(16)、式(19)、式(22)代入式(24)中,可以得到单元的动力学方程为

(25)

对于n-1个ANCF单元而言,其共有n个不同的特征节点。结合式(25)可以得到整体的动力学方程为

(26)

式(26)中：Ci为第i个单元的阻尼系数矩阵;Ki为内层的线弹性力矩阵;QLayerIIi为外层的弹性力矩阵;Qi为外力矩阵;qi为广义坐标矩阵;i=1,2,…,n。

在此基础上,利用布尔逻辑型矩阵B可以得到如式(27)所示的转换关系。

(27)

式(27)中：w为各个节点位置处的广义坐标所组成的列阵,其不包含重复节点。

于是式(26)可进一步改写为

(28)

(29)

3 数值方法

3.1 子域积分的数值方法

对于第2节中所涉及的体积分问题实质上很难得到一个准确的解析解。在Matlab程序调试当中利用Syms符号函数进行积分求解会极大地降低工作效率。为此,采用Gauss-Legendre数值积分策略,先利用坐标变换将空间圆柱型积分域变换成严格的高斯型积分域,再取用5个×5个×5个高斯积分点精确的求解相应的空间体积分问题。5个×5个高斯积分点在平面上的位置排布如图4所示。

图4 5×5高斯积分点在平面上的分布

内芯层体积分可以改写成式(30)所示的形式。

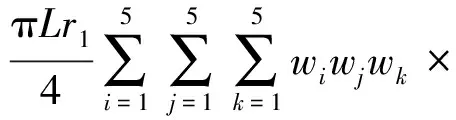
(30)

式(30)中：F为以笛卡尔坐标为自变量的待积函数;r1为内芯层圆截面的半径;r为缆索单元的半径;Φ为积分的转角变量;L为缆索单元的长度;Ai、Bj、Ck为对应序号的高斯积分点;wi、wj、wk为对应积分点的权重系数。

同理,护套层体积分可以改写成

(31)

式(31)中：r2为缆索单元截面的半径。

3.2 动力学求解的数值方法

为保证微分方程数值求解的稳定性,避免出现由于方程刚性较强而产生的失稳现象,利用隐式方法进行数值求解,这是因为相较于显示方法而言,隐式法的稳定域通常更大,不必选用过分小的步长来满足苛刻的稳定性条件。但是任何隐式方法均涉及非线性方程组解的数值迭代,其实现过程复杂、计算效率低下。为此,设计一种具有隐式效果的差分格式,以便对上述动力学微分方程组进行高效准确的数值求解。

将式(28)进行等价性变换得

(32)

式(32)中：υ为各个节点位置处的广义速度所组成的列阵,其不包含重复节点。

一阶隐式欧拉法的格式可以写为

(33)

式(33)中：wi、vi分别为ti时刻下的位移变量与速度变量;h为固定的时间步长。

(34)

式(34)保留了部分隐式方法的基本特征,但却是一种显示差分格式,其在扩大稳定域的同时改善了原来隐式方法求解效率低的特征。

3.3 静力学求解的数值方法

为提高非线性方程组数值迭代的收敛速度,因此采用Newton-Raphson方法进行数值迭代。将式(28)进行等价性变换得

(35)

其迭代格式可以写为

(36)

4 数值算例

4.1 静力学数值仿真

为了将相关理论解同数值解进行对比,选用静态小变形问题进行说明。将水平力与垂直力分别施加在悬臂缆的自由端,并分析自由端位移的变化情况。其中,水平力Fh与垂直力Fv的大小均为10 N。受力情况如图5所示。模型的基本参数如表1所示。

表1 仿真参数Table 1 Parameters of simulation

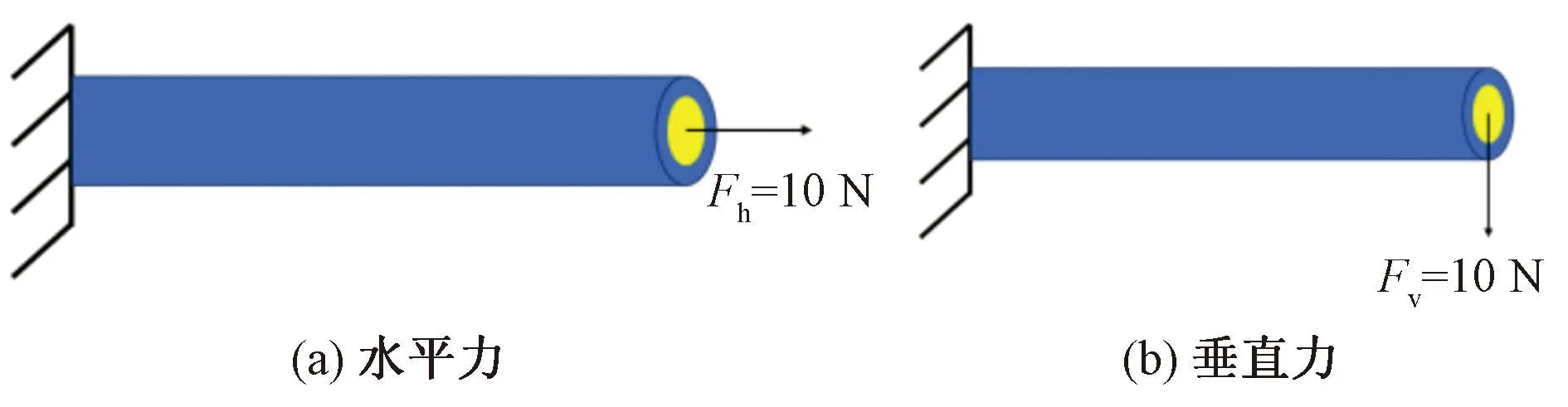
图5 两个小变形问题

在水平力Fh的作用下,末端伸长量Δl在小变形静力学问题下的理论解为

(37)

式(37)中：E1、E2分别为内、外层材料的杨氏模量;Δl=1.586 6×10-7m。

利用Newton-Raphson迭代的结果如表2所示。

表2 水平力下的数值解Table 2 Numerical solution under horizontal force

在垂直力Fv的作用下,挠度w在小变形静力学问题下的理论解为

(38)

其具体的数值结果为w=2.100 7×10-3m。利用Newton-Raphson迭代的结果如表3所示。

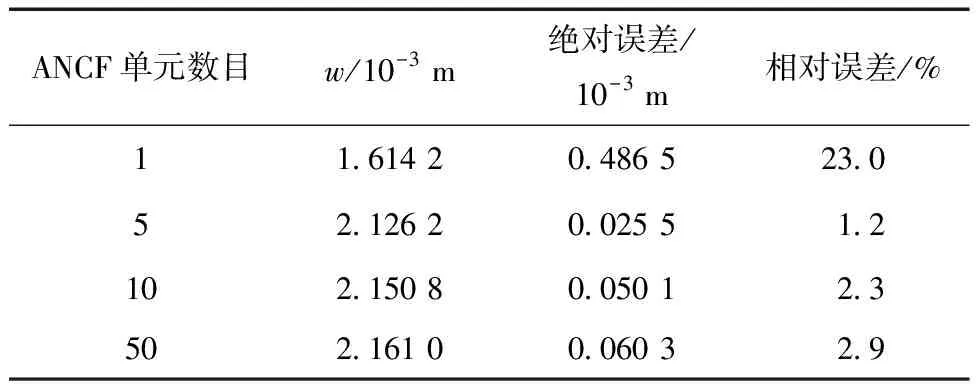
表3 垂直力下的数值解Table 3 Numerical solution under vertical force

由表2、表3可知,ANCF单元数目的增加使得仿真解更加贴近理论解。自由端位移的精度与收敛性得到了一定的保证。

ANCF单元的数目为5个时,挠度迭代的基本情况如图6所示。而对于应用Mooney-Rivlin模型与原始的Yeoh模型的ANCF单元而言,迭代过程中数值解的变化规律如图7所示。

图6 垂直力下挠度解的迭代

图7 两种模型下数值解的迭代

由图6、图7可知,应用Mooney-Rivlin的单元迭代收敛的速度较慢,而对于应用另外两种模型的单元而言,数值迭代均能够快速、高精度地收敛到正确解。

4.2 动力学数值仿真

4.2.1 物理摆

水平放置的柔性摆在重力的作用下下落,研究系统的动力学响应特征以及能量的变化规律。柔性摆的基本参数如表4所示。偏应力耗散因子与膨胀应力耗散因子分别取0.01与0.1。

表4 缆索的基本参数Table 4 Parameters of cable

图8为摆的自由端沿着x、y方向的位移变化曲线。图9为摆落过程中动能、重力势能、应变能以及耗散能随时间的变化规律。

图8 自由端的位移

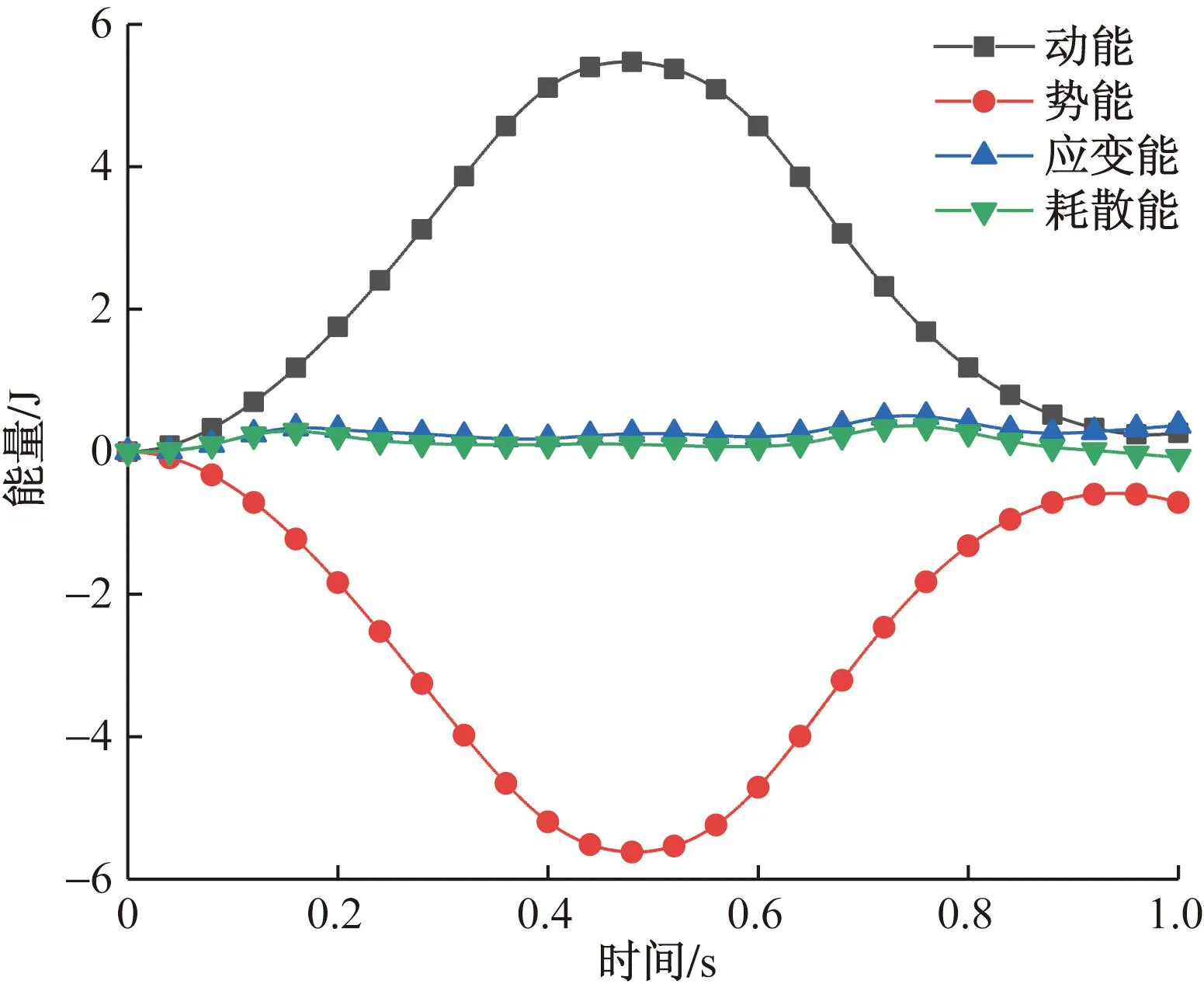
图9 能量的变化情况

由图9可知,能量的变化规律符合预期的结果。动能与重力势能呈现出反相的基本特征,即系统的动能取极大值时,重力势能取极小值。这是由于柔摆下落过程中势能主要向动能转化,仅有一小部分经过阻尼力耗散后的能量转化成了单元内部的应变能。总体来说,系统的总能量在整个模拟时间内保持不变,单元具备能量守恒的基本特征。这也证明了动力学数值方法的可行性与单元动力学响应的可靠性。

4.2.2 悬臂缆的摆落

主要探究应用几种不同的不可压缩材料模型对单元数值响应的影响,这是因为不同的超弹性解释模型在大变形、强非线性特征下的力学特性各有差异。表4给出了缆索的基本参数信息。

图10为应用3种不可压缩材料模型的ANCF单元于不同时刻的位形曲线。可以看出,应用改进后Yeoh模型的单元于不同时刻下的位形曲线与原始Yeoh模型结果高度一致。这意味着原始Yeoh模型和改进后Yeoh模型对单元动力学行为的影响效果基本一致。而对于应用Mooney-Rivlin模型的ANCF单元而言,其自由端的位移随着时间的不断推移明显超前于应用另外两个模型的缆索单元。其势能转化为动能的速度更快。在总能量守恒的前提下,Mooney-Rivlin模型所产生的应变能低于原始Yeoh模型和改进后Yeoh模型,导致其无法准确地反映柔性缆在大尺度变形下的运动情况。

图10 应用3种不可压缩模型的单元的位置构型

5 结论

提出一种适用于线缆动力学建模的ANCF缆索单元。其中利用Kelvin-Voigt模型来解释内层结构的黏弹性性质,而将改进的Yeoh模型应用于护套层单元当中。在此基础上,通过一系列静力学与动力学数值仿真得到如下结论。

(1)单元能够高精度快速地收敛到理论解,并且对比了应用3种不可压缩模型的单元的收敛特性,证实了本单元具备较好的收敛性能。

(2)通过柔性摆的数值模拟证实了单元具备能量守恒的基本特征,证明了数值方法的可行性与单元动力学行为的可靠性。

(3)应用改进的Yeoh模型的单元能够很好地反映柔性缆在大尺度变形下的运动。而相较于应用Mooney-Rivlin模型的ANCF单元而言,其无法准确地反映柔性缆在大变形条件下的运动特征,进一步证实了所提出的ANCF缆索单元的合理性与优越性。