C3连续的保形分段二次三角 Bézier插值曲线

朱秀云,吴晓勤,陈福来

(湖南科技大学 数学与计算科学学院,湖南 湘潭411201)

引言

在几何造型中,曲线的保形插值有着非常关键的作用.常见的C1连续的三次Hermit插值及C2连续的五次Hermit插值,均不一定保形[1].目前的研究成果有GoodmanT.N.T.提出的曲率连续的分段三次保形插值法[2,3];方逵等利用三次Bézier曲线构造了G2连续的保形分段三次插值曲线[4];康宝生构造了C1连续的分段有理三次保凸插值[5];朱晓临构造了C3连续的保凸插值T-B曲线[6];我们构造了C3连续的保形插值三角样条曲线[7].

若给出一组有序点列 Si(i=0,1,…,n)及每个点处的相应切矢Ti,通常可用参数三次曲线来进行C1的Hermit插值[8],若需要更高的连续阶,则要求提供更高阶的导矢.但高次曲线不但计算复杂,且需要较多的数据存储,同时曲线的几何形状很难控制(拐点太多),因此,高次几何参数曲线很难应用于实际.三次Bézier曲线很容易构造C2连续的插值曲线.然而,当控制多边形给定后,Bézier曲线的形状也就惟一确定,若需调整Bézier曲线,则需修改Bézier曲线的控制顶点.为了更有效地对曲线进行调控,不少学者研究推广了Bézier曲线.在众多的推广形式中,由于三角样条基函数含有三角函数,所以由它们构造的一些曲线就很容易表示圆锥曲线和一些超越曲线.就三角多项式样条曲线与通常的多项式样条曲线相比,具有连续性好,逼近度高,还可精确表示圆和椭圆等特性.因此,近年来,利用三角多项式研究保形插值成为一个热点.人们发现基于四点的二次三角Bézier曲线有许多优良性质,且完全具有三次Bézier曲线的特性,所构造的曲线能够更好地逼近控制多边形.因此,在外形设计中,二次三角 Bézier曲线越来越受到重视,有着较为广泛的应用前景.

本文利用二次三角Bézier曲线,构造出一保形插值且C3连续的曲线,同时曲线的形状能方便地由形状参数作局部调整.

1 二次三角Bézier曲线

文献[9]给出了二次三角Bézier曲线的定义.

设Si(i=0,1,2,3)为平面上的一组给定的控制顶点,定义曲线

为二次三角Bézier曲线,其中基函数Bi(t)定义为

这里λ为参数,且−1≤λ≤1.

由(2)式可导出曲线l( t)具有如下重要性质:

(1)端点性质,即

说明曲线具有与三次Bézier曲线完全相同的端点性质:插值首末两个端点且与端点相切.

(2)对称性,凸包性,几何不变形,变差缩减性,保凸性.

2 保形插值曲线的构造

设Si(i=0,1,…,n)是一组给定的平面型值点,用直线段连接相邻两点构成一型值多边形为＜S0,S1,…,Sn＞,记其边向量分别为ai= Si−1Si(i=1,2,…,n).

定义1已知型值多边形＜S0,S1,…,Sn＞,如果ai−1×ai与ai×ai+1反向,则称Si是多边形＜S0,S1,…,Sn＞的拐点;否则无拐点.

定义2如果曲线l(t)∈C3[a,b],插值点为Si(i=0,1,2,…,n),且满足如下条件:

(1)型值多边形＜S0,S1,…,Sn＞为凸时,l(t)也为凸,且凸向一致;

(2)l(t)在型值多边形＜S0,S1,…,Sn＞ 的拐点处有一个拐点,则称l( t)为参数区间[a,b]上的C3保形插值曲线.

2.1 型值点处切矢的确立

由型值多边形的边向量定义,插值曲线在Si处的切矢Ti定义如下

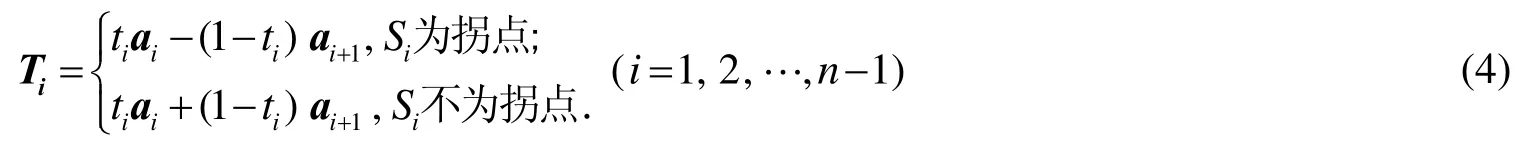
若型值多边形＜S0,S1,…,Sn＞是开的,则

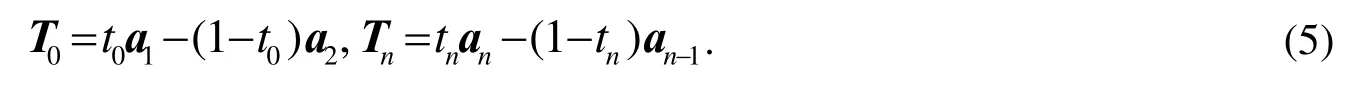
若型值多边形＜S0,S1,…,Sn＞是闭的,即 Sn=S0,则

其中0＜ti＜1 是切矢调节参数.

根据切矢Ti的定义,通过调节切矢参数使Ti与Ti+1不平行,从而有以Ti为切矢过点Si的切线与以Ti+1为切矢过点Si+1的切线相交,记交点为

图1 新控制多边形的构造

2.2 分段二次三角Bézier曲线的构造

通过在每相邻两个插值点之间构造一段二次三角 Bézier曲线,使相邻段之间是 C3连续的和保形的,从而构造出一条插值所有型值点且保形的二次三角 Bézier曲线.若曲线是闭的,仅令 Sn=S0,Sn+1=S1,Sn+2=S2即可.记图1中过Si−1,Si的二次三角Bézier曲线段为 li(t)(i= 1,2,…,n).li(t)的四个控制顶点为

其中0＜ωi,μi＜1是可调参数.

又由二次三角Bézier曲线的端点性质(3),易知 li( t)与 li+1(t)在Si点达到位置连续.

下面讨论C1,C2连续条件.先讨论C1连续的条件,要求

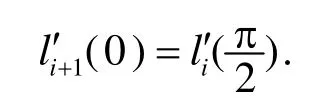
由性质(3)有

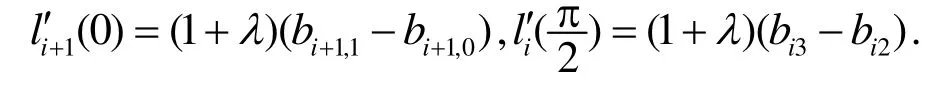
经计算有

将式(8)代入上式,可得

下面讨论C2连续的条件.根据文献[9],首先要求λ=1.

对于曲线l( t)在满足 C0,C1连续的条件下,若曲线l( t)在各型值点处达到 C2连续,必须有,再由性质(3)有

即

结合式(8)、(9)有

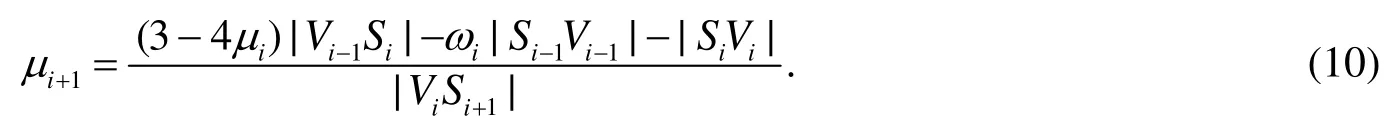
定理 1当参数λ=1,如果在满足式(9)的条件下,再满足式(10)和(11),则曲线l( t)在各型值点处达到C3连续.

证明由曲线的端点性质知,曲线l( t)在各型值点处达到C2连续,则自动达到C3连续.

li(t)的四个控制顶点 bij(j=0,1,2,3)构成一个控制多边形＜bi0bi1bi2bi3＞,由二次三角 Bézier曲线的保凸性知,若此控制多边形为凸的,则 li(t)显然也是凸曲线段,且凸性与＜Si−1Vi−1Si＞一致.如果型值点Si为拐点,即矢量 Si−2Si−1× Si−1Si与矢量 Si−1Si×SiSi+1反向,此时第i段曲线与第i−1段曲线凸性相反,且在Si处形成一个拐点.因而构造的分段二次三角 Bézier曲线拐点与给定型值多边形的拐点个数相同,从而该曲线对其给定的型值多边形是保形的.综上知,插值曲线l( t)是 C3连续和保形的,同时曲线形状的局部调整很方便,如通过改变 ti,ωi,μi的值便可调整第i段曲线 li(t)的形状,而且曲线段 li(t)的调整最多仅影响其相邻两段曲线,却与别的曲线无关.

特别地,若 Si−1,Si,Si+1三点共线,则可定义 Ti−1= Ti= Ti+1=ai,此时Si−1Si+1为一直线段,构造的曲线依然是保形的,如图2中的线段S0S4.

3 算法步骤

给定平面上的一组有序点列 Si(i=0,1,…,n),构造保形插值二次三角Bézier曲线l( t)的算法如下:

Step1根据定义1确定型值多边形的拐点;

Step2由(4)、(5)、(6)三式确定插值曲线在各型值点处的切矢;

Step3由(7)式计算相邻两型值点切线的的交点 Vi(i=0,1,…,n−1);

Step4在区间(0,1)内选定μi,由式(11)选定ωi,再由式(10)确定μi+1,式(9)确定ωi+1,最后结合式(8)确定bij( i=1,2,…,n,j=0,1,2,3);

Step5以bij(j=0 ,1,2,3)为控制多边形顶点,按(1)式计算第i段曲线 li(t)上的点;

Step6调节参数ti(i=0 ,1,2,…,n),转2、4步,可修改曲线的形状.

该算法构造的曲线是C3连续的,该曲线既解决了二次三角Bézier曲线的构造问题,又是一种保形插值的有效方法.通过该算法,由型值点直接计算所有控制点,而无需求解线性或非线性方程组,且曲线的构造有很好的局部性.

4 数值实例

例1用本文方法对Akima数据点作保形插值,如图2所示.图2中圆点为Akima数据点,插值曲线分为两部分,一部分为直线段,另一部分是曲线.

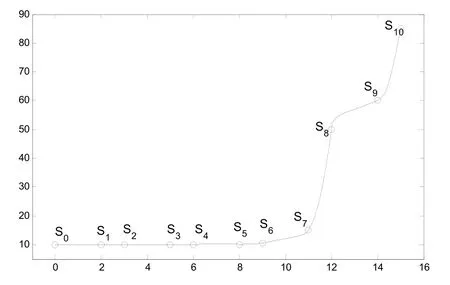
图2 插值Akima数据点的二次三角Bézier曲线

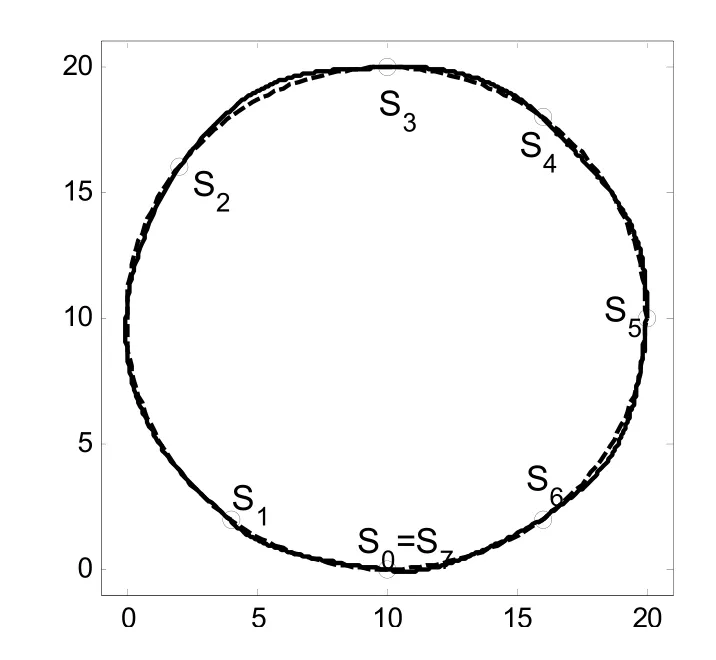
图3 插值封闭圆上数据点的二次三角Bézier曲线

例2给定一整圆上的数据点列S0(10,0),S1(4,2),S2(2,16),S3(10,20),S4(16,18),S5(20,10),S6(16,2),S7(10,0),对该点列进行C3连续的分段二次三角 Bézier保形插值.如图 3所示,其中实线是得到的插值曲线,虚线是一个整圆.

[1] W.Boehm,etal.A Survey of Curve and Surface methods in CAGD[J].Computer Aided Geometric Design,1984,39(1):1～60

[2] Goodman T.N.T.,Unsworth k.Shape preserving interpolation by parametrically defined Curves[J].SLAM J.Numerical Anal ,1988,25(6):1～13

[3] Goodman T.N.T.,Unsworth k.Shape preserving interpolation by curvature continuous parametrically defined curves[J].Computer Aided Geometric Design,1988,15:323～340

[4] 方 逵,文 锦.(G2-连续的)保形分段三次插值曲线[J].工程数学学报,1999,16(3):6～16

[5] 康宝生.分段有理三次保凸插值[J].高等计算数学学报,1995,17(2):138～144

[6] 朱晓临,葛传丰.C3连续的保凸T-B插值曲线及保形插值算法[J].工程图学学报,2009,(6):76～80

[7] 吴晓勤.C3连续的保形插值三角样条曲线[J].数学理论与应用,2002,22(1):60～64

[8] Farin G.Curves and Surfaces for Computer Aided Geometric Design:A Practical Guide [M].Academic Press,1988

[9] 吴晓勤.带形状参数的二次三角Bézier曲线[J].工程图学学报,2008,(1):82～87