行列式几何化的教学研究

陈志彬，张爱平，李 强

(湖南工业大学理学院应用数学系，湖南株洲412000)

行列式几何化的教学研究

陈志彬，张爱平，李 强

(湖南工业大学理学院应用数学系，湖南株洲412000)

基于向量内积与外积的几何意义，将行列式用向量的这2种运算形式表示，揭示空间中由向量构成的平行四边形的面积或平行多面体的体积与行列式之值的关系，将行列式几何化，丰富直观教学内容，探索行列式教学的新途径。

行列式;几何化;超平面;超平行多面体

行列式是线性代数中的一个重要内容，是教学中的难点和重点，线性代数中的许多概念都与行列式密切相关，掌握好行列式是学好线性代数的关键。目前，国内编写的线性代数教材把行列式的内容都放在第一章，多数教材是以消元法求解二元或三元线性方程组引入行列式概念的，把线性方程组的解化归为统一形式，将求解问题转化为单纯的计算行列式的问题，向学生演示引入行列式概念的背景知识，表明线性方程组与行列式存在某种代数运算关系。然而，这些却未能将几何与代数有机结合起来，向学生呈现出蕴含的几何背景知识，让学生从几何的角度更好地理解线性方程组的解;特别是关于行列式的性质，多数教材仅以代数的各种运算关系给出介绍与证明，利用定义证明行列式性质的纯代数方法常常令学生感到抽象;在行列式教学中，多数教师仅重视计算行列式的运算技巧而忽视行列式的几何解释，让学生难以接受。因此，针对行列式教学中存在的这些不足，本文用类比法将行列式与向量相结合，在欧氏空间中通过引入正交坐标系，用向量的内积和外积的运算形式表示行列式的值，或用投影降维的方法探索行列式与多个平行多面体的关系，将行列式几何化，从而改革关于行列式传统的教学方法和内容，促进学生的直观思维，化代数抽象问题为几何的具体问题。

一 向量的内积、外积与行列式几何化的关系

向量是一个既有大小又有方向的量，是一个几何概念的量。由于引入笛卡尔坐标系，把向量表示成关于坐标的有序数组，实现了向量的几何运算向代数运算的转化。向量的加法、减法、内积和外积4种运算成为超越坐标几何的有力工具，使得坐标系中不能进行运算的点具有了按向量运算的功能。因此，利用向量，巧妙地解决了直线与直线的垂直或平行关系、空间中线面或面面之间的位置关系等几何问题，实现了数形的完美结合。行列式在本文中被作为关于向量的一张表，其定义看成是表上的一种算法，行列式的值与表中向量组成的几何图形相对应，按照对行列式几何化的这一思路，首先在二维和三维空间中讨论行列式的几何化问题，然后将其推广到高维空间，最后获得行列式统一的几何化的结论。

便于后面讨论，首先介绍向量的内积和外积的概念及几何解释。在三维空间中，设x、y和z轴的单位正向量分别用 i﹑ j﹑ k 表示，已知向量 a=(ax，ay，az)，b=(bx，by，bz)，根据向量的内积运算定义:

向量的外积运算定义如下:

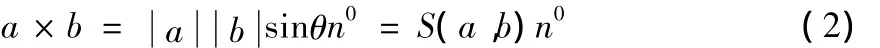
其中θ(0≤θ≤π)为向量a到b所成的角，S(a，b)表示a，b 2个向量张成的平行四边形的面积，n0是依右手法则垂直于由向量a到b所张成的平面的单位法向量。式(2)的几何解释是a×b表示一个新的向量，大小等于向量a﹑b张成的平行四边形的面积S(a，b)，方向垂直于a到b所张成的二维平面。由此可知，在坐标运算中外积的概念只适合于三维及三维以上的向量空间，2个向量的外积等于他们所张成的平行四边形的有向面积S(a，b)n0，在三维向量空间中，利用(2)式，可得x、y和z轴的单位正向量i﹑j﹑ k的外积运算式:i× j=k，j× k=i，k× i=j，以及向量a与b的外积运算式:

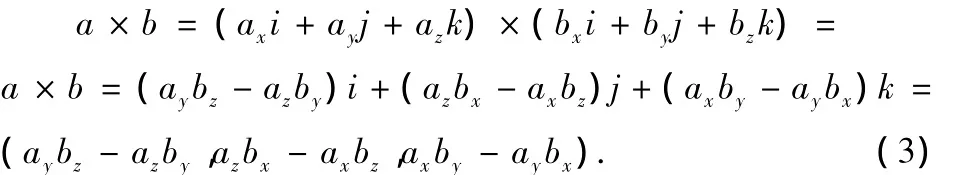
利用二阶、三阶行列式又可把(3)式改写成关于x、y和z轴上三个向量的线性组合形式

在(2)式中，如果令法向量n0与x、y和z轴所成的角分别记为 θ，β，γ，则单位法向量 n0=(cosθ，cosβ，cosγ)，其中jcosβ+kcosγ)，由此可得:向量a×b的坐标则具有如下的几何解释:

(ⅰ)当Ax＞0(Ax＜0)时，表明cosθ＞0(cosθ＜0)即单位法向量n0指向x轴的正向(x轴的反方向)，Ax为向量a﹑b张成的平行四边形在yoz坐标平面上的有向面积投影。

(ⅱ)当Ay＞0(Ay＜0)时，表明cosβ＞0(cosβ＜0)单位法向量n0指向y轴的正向(y轴的反方向)，Ay为向量a﹑b张成的平行四边形在zox坐标平面上的有向面积投影。

(ⅲ)当Az＞0(Az＜0)时，表明cosγ ＞0(cosγ ＜0)单位法向量n0指向z轴的正向(z轴的反方向)，Az为向量a﹑b构成的平行四边形在xoy坐标平面上的有向面积投影。

二 二维和三维空间中行列式的几何化

下面将向量张成的平行四边形的有向面积或平行多面体的有向体积，用降维的方法向坐标面投影，讨论二阶行列式和三阶行列式几何化的问题。

可从向量的三维空间和二维空间2个角度对二阶行列式做出如下几何化解释:

ⅰ)在三维空间中，取向量的第三个坐标为零，即向量a1=(a11，a12，0)，a2=(a21，a22，0)，向量 a1与 a2张成的平行四边形落在xoy坐标面上，通过增加向量的维数，由坐标面上的平行四边形看成是由三维空间中的向量a1与a2张成的平行四边形在xoy坐标面上的投影，这个平行四边形的有向面积为S(a1，a2)k，二阶行列式的值为S(a1，a2)，如果S(a1，a2)＞0，则表明按右手法则选择以向量a1的方向为始边，依逆时针转过一个θ(0≤θ≤π)角达到向量a2，右手拇指的指向与z轴的正方向一致;如果S(a1，a2)＜0，则按右手法则选择以向量a1的方向为始边，依顺时针转过一个θ(0≤θ≤π)角达到向量a2，右手拇指的指向与z轴的反方向一致;如果S(a1，a2)=0，则向量a1与向量a2共线。

ⅱ)在二维空间中，取向量 a1=(a11，a12)，a2=(a21，a22)，引入记号，其中向量ai(i=1，2)在x轴上的坐标记为 ai1(i=1，2)，向量ai(i=1，2)在y轴上的坐标为ai2(i=1，2)，行列式的值表成了行列式的2个行向量在x轴上的坐标与在y轴上的坐标之间乘积的代数和，而数a11a22与 －a12a21分别对应2个矩形的有向面积。对于第一项a11a22，如果a11a22＞0，则表明以向量)为始边，依逆时针转过一个θ(0≤θ≤π)角达到向量)，如果a11a22＜0，则表明以向量为始边，依顺时针转过一个θ(0≤θ≤π)角达到向量;对于第二项 －a12a21，如果－a12a21＞0，则表明以向量为始边，依逆时针转过一个θ(0≤θ≤π)角达到向量，如果－a12a21＜0，则表明以向量为始边，依顺时针转过一个θ(0≤θ≤π)角达到向量

ⅰ)在三维空间中，用向量的外积运算对行列式的性质解释如下:

令三维向量 a1=(a11，a12，0)，a2=(a21，a22，0)，a3=(a21+ka11，a22+ka12，0)，则 a1× a3=a1× (a2+ka1)=

这表明向量a1与向量a3张成的平行四边形的有向面积与向量a1与向量a2张成的平行四边形的有向面积相等。

ⅱ)在二维空间中，可作如下几何解释:

二维向量 a1=(a11，a12)与 a3=(a21+ka11，a22+ka12)张成平行四边形是由向量a1=(a11，a12)与a2=(a21，a22)张成平行四边形在保持同底同高的情况下发生切变所得，这2个平行四边形的面积相等，法向量的方向不变。

利用(1)(2)中的方法，对二阶行列式的其它性质同样可以做出类似的几何解释，故略去．下面探讨三阶行列式几何化的问题:

问题3:三阶行列式

ⅰ)设三维向量 a(1)=(a11，a12，a13)，a(2)=(a21，a22，a23)，a(3)=(a31，a32，a33)，则有代数等式 (a(2)× a(3))·

或者有等式 (a(2)× a(3))·a(1)=S(a(2)，a(3))［a11cosθ+a12cosβ+a13cosγ］，即三阶行列式与三个向量间的混合积的的运算相联系，(a(2)×a(3))·a(1)对应着一个几何图形，表示以3个向量a(1)、a(2)和a(3)为棱长所张成的平行六面体的有向体积。基于代数式S(a(2)，a(3))n0·a(1)分2种情形解释如下:

第一种情形:外积a(2)×a(3)=S(a(2)，a(3))n0表示以坐标原点为始点的2个向量a(2)到a(3)所张成的平行四边形的有向面积，单位法向量n0的指向由向量a(2)旋转到向量a(3)的方向确定，如果平行四边形是以向量a(2)为始边依顺时针转过一个θ(0≤θ≤π)角到向量a(3)张成的，则单位法向量n0指向平行四边形的下侧，如果向量a(1)的方向与单位法向量n0垂直，则向量a(1)与向量a(2)，a(3)共面，三阶行列式的值S(a(2)，a(3))n0·a(1)=0;如果平行四边形是以向量a(2)为始边依逆时针转过一个θ(0≤θ≤π)角到向量a(3)张成的，则法向量n0指向平行四边形的上侧;n0?a(1)为向量a(1)在单位法向量n0上的投影，如果向量a(1)的方向与单位法向量n0同侧，则三阶行列式的值S(a(2)，a(3))n0·a(1)为正，其值等于这3个向量所张成的平行六面体的体积，如果向量a(1)的方向与单位法向量n0异侧，则三阶行列式的值S(a(2)，a(3))n0·a(1)为负，等于这3个向量所张成的平行六面体的体积的相反数。

第 二 种 情 形:由 n0· a(1)=[a11cosθ+a12cosβ +a13cos γ ]得三阶行列式等于向量a(1)的3个坐标分别乘以一个相应的二阶行列式的代数和，代数和式中的每个部分都对应着一个特定的小平行六面体的有向体积，其中，它表示a(2)到a(3)所张成的平行四边形的有向面积在坐标平面yoz上的有向投影S(a(2)，a(3))cosθ乘以向量a(1)在x轴上的坐标a11，同理第二部分和第三部分分别表示a(2)到a(3)所张成的平行四边形的有向面积在坐标平面zox上的有向投影面积乘以向量a(1)在y轴上的坐标a12，在坐标平面xoy上的有向投影面积乘以向量a(1)在z轴上的坐标a13．因此，由3个向量在三维空间中所张成的平行六面体的有向体积等于底在坐标平面上高在坐标轴上的3个小的平行六面体的有向体积之和。

问题4:三阶行列式另一种代数形式

a13a22a31－a11a23a32－a12a21a33的几何化问题。

在问题3中将二阶行列式展开可得到上面三阶行列式的另一种代数形式，等式中共有六项，每一项由来自3个向量中的不同坐标的3个数相乘，其中有三项的符号为正，其余项的符号为负，对应着将原三阶行列式分解成如下的由坐标向量构成的六个三阶行列式的代数和，即由3个向量a(1)、a(2)和a(3)的坐标向量作混合积得到:

增加向量的维数，类似于将几何图形由三维投影到二维解释二阶行列式的方法，同理在四维空间中亦可解释三阶行列式的几何化问题。首先建立四维正交坐标系，设正交单位坐标向量 e1=(1，0，0，0)，e2=(0，1，0，0)，e3=(0，0，1，0)e4=(0，0，0，1)，其中任意一个向量由其余3 个向量通过下列形式定义的外积运算得到:

用增加向量维数的方法，再将原3个三维向量a(1)、a(2)和a(3)中的坐标增加一个，增加的第四个坐标都为0，不妨得到相应的3个四维向量仍记为a(1)、a(2)和a(3)，这三个四维向量的外积a(1)×a(2)×a(3)是一个新的向量，通过计算得等式:，因此，三阶行列式是由3个四维向量a(1)、a(2)和a(3)所张成的超平行多边形的有向面积，也可以解释为在四维空间中由3个向量张成的有向超平行多边形在三维空间上的有向投影。如果三阶行列式的值为正，则有向超平行多边形的方向指向坐标轴e4的反方向，如果三阶行列式的值为负，则有向超平行多边形的方向与坐标轴e4的方向一致。

在上面的讨论中得到:行列式对应着平行四边形的有向面积或平行多面体的有向体积，并且可以分解成由坐标向量构成的若干个简单行列式的代数和，即二阶行列式的有向面积等于2个小长方形的有向面积之和，三阶行列式的有向体积等于6个小长方体的有向体积之和，而决定每一个面积块或体积块的符号(方向)与乘积项中元素的排列顺序有关;若将向量的维数增加一维，则低一维空间中的有向平行多面体可看成高一维空间中的有向超平行多边形。

三 n维空间中n阶行列式的几何化

根据人的思维具有流畅性的特性，三阶行列式能用2个三维向量的外积再与一个向量的内积得到，即向量的混合积(a(2)×a(3))·a(1)表示，学生自然会提出一个问题:一个n阶行列式用n维向量有类似的表示吗?在一般的线性代数教材中都回避了这个问题，使得学生对行列式具有的共性缺乏认识，产生疑惑。实质上n阶行列式仍然可以用n－1个n维向量的外积再与一个向量的内积得到，将它化归为向量运算的一个统一问题。下面引入n维正交坐标系，利用向量的外积与内积运算揭示n维向量与n阶行列式的关系。

在n维欧氏空间中，单位正交坐标向量记为

其中任意一个坐标向量用其余的n－1个坐标向量的外积定义如下:

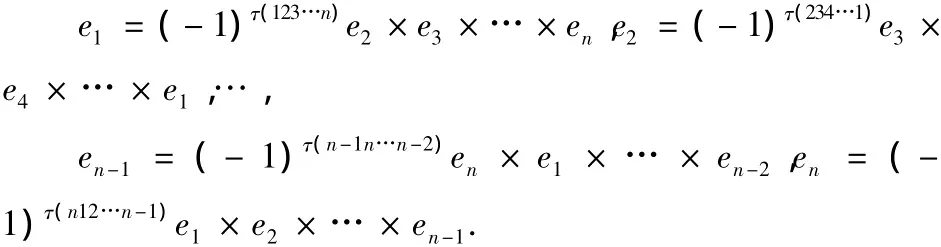
τ(i1i2…in)表示i1i2…in排列的逆序数。

根据向量的运算，任意一个n维向量可表为坐标向量的代数和，于是用坐标向量表成的n－1个n维向量的外积a(2)×a(3)×…×a(n)在以上n－1个坐标向量定义了外积的前提下则是有意义的，它仍是一个n维向量，其向量的长等于这n－1个n维向量张成的超平行多边形的面积S(a(2)，a(3)，…，a(n))，而外积等于超平行多边形的面积S(a(2)，a(3)，…，a(n))乘以超平行多边形的单位法向量n0，通过简单计算，用一个n阶行列式表示如下:

因此，对n－1个n维向量进行外积运算后再与一个n维向量进行内积运算易得到一个数值，故略去计算过程，这个数值对应着一个n阶行列式:

上式可作如下几何解释:它表示以有向超平行多边形S(a(2)，a(3)，…，a(n))n0为底，向量 a(1)的长为棱构成的有向超平行多面体的体积。如果n阶行列式的值为正，则表明向量a(1)的方向与超平行多边形的方向同侧:如果n阶行列式的值为负，则表明向量a(1)的方向与超平行多边形的方向异侧:如果n阶行列式的值为0，则表明向量a(1)与超平行多边形共面。

四 应用举例

将行列式几何化的思想应用到几何中，能巧妙的把向量与平面或多面体结合起来，对获得的结果赋以新的几何解释，下面以几何中常见的几个问题为例，对这些简洁的结论用行列式的几何解释说明，旨在抛砖引玉。

解:这个问题若用常规方法，通过求平行四边形的底和高来求其面积，则显得繁琐;若是依照三维空间中两个向量外积的几何解释来求，则是一种简单的运算，即由下式得

例2．用行列式表示过平面上已知两点 A(x1，y1)，B(x2，y2)的直线方程．

解:在过 A、B 2点的直线上任取一点 C(x，y)，则A、B、C 三点共线当且仅当(其中λ为常量)成立．由于对二维向量不能进行外积运算，因此，用增加向量的维数方法，将 A、B、C 的坐标扩展到三维即为 A'(x1，y1，1)，B'(x2，y2，1)，C'(x，y，1)且同样满足共线的条件则这3个向量张成的几何图形是共面的，相当于3个向量张成的平行多面体被压缩成一个平面，其体积等于零。于是有直线的行列式形式．实质上学生由直线的两点式很容易得到直线方程，在高中就已经学习过，但是，以此为例能较好地让学生领会直线方程与行列式和一个几何图形的变化关系。

用同样的方法可推得:过空间中不共线的三点A(x1，y1，z1)，B(x2，y2，z2)，C(x3，y3，z3)的平面方程，其行列式形

类似例2的解释作同样的处理，即在A、B、C所在的平面上任取一点 D(x，y，z)，对 A、B、C、D 增加第 4 个坐标且都为1，则得到 4 个四维坐标的点，相应记为 A'，B'，C'，D'由点A、B、C、D共面，推得四维向量3个四维向量所张成的超平行多边形共面，相当于4个四维向量张成的超平行多面体被压缩成一个平面，故其体积等于零。

总之，将行列式几何化引入教学，这能更好地让学生领会到行列式的应用，有利于学生在后续学习向量的线性相关性和线性变换等知识时，自觉地从几何的角度思考问题，较好地理解线性代数中诸多抽象的概念。

［1］周 勇，朱 砾．线性代数［M］．上海:复旦大学出版社，2010．

［2］陈志杰．高等代数与几何［M］．北京:高等教育出版社，2008．

［3］谢 琳，张 静．从几何直观理解行列式与Cramer法则［J］．高等数学研究，2009，12(1):61 －62．

［4］李尚志．从问题出发引入线性代数概念［J］．高等数学研究，2006(6):15－17．

O1512

A

1674－5884(2012)04－0090－05

2012－03－10

湖南省教育科学研究项目(10C0656);湖南工业大学教学改革项目(09E65)

陈志彬(1965－)，男，湖南邵阳人，副教授，硕士，主要从事泛函微分方程研究。

(责任编校 晏小敏)