设而不求在立体几何中的应用例举

☉甘肃省兰州女子中专 施梅兰

有些数学题，看似缺少条件，但如果恰当地引入参数，建立起已知条件与所求答案之间的关系，但在解题过程中，这些参数始终避而不求，而是通过巧妙运算，精妙构造，使参数“悄然离去”，实现解题目的.这就是“设而不求”的思想.本文仅就“设而不求”思想在立体几何中的应用进行归纳总结，以供参考.

一、线线角问题

例1如图1，OA是圆锥底面中心O到母线的垂线，OA绕轴旋转一周所得曲面将圆锥体积分成相等的两部分，求圆锥母线与轴的夹角α.

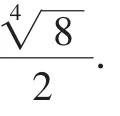
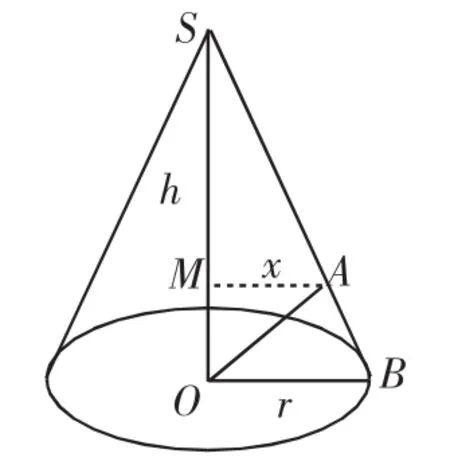
图1

图2

二、二面角问题

例2在三棱锥V-ABC中，VA∶VB∶VC∶BC=4∶3∶3∶2，且VA⊥VB，VA⊥VC.求二面角V-BC-A的大小.

解：如图2，取BC的中点D，连接VD，AD，因为VB=VC，所以VD⊥BC，又VA⊥VB，VA⊥VC，VA⊥平面VBC，AD⊥BC，∠ADV为二面角V-BC-A的平面角.

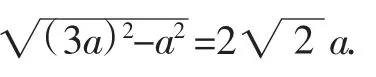
三、线段长问题

例3已知长方体的全面积为11，十二条棱长度之和为24，求这个长方体的对角线长.

解：设过一顶点的三条棱长分别为x，y，z，长方体的对角线的长为l，则：

因此，这个长方体的对角线长是5.

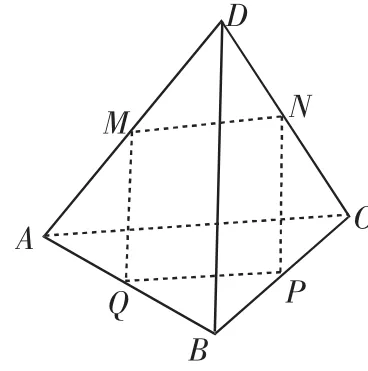
图3

四、周长问题

例4如图3，用平行于四面体ABCD一组对棱AC、BD的平面截此四面体得到四边形MNPQ，若AC=BD=p，求四边形MNPQ的周长.

解：设MQ=x，PQ=y，AM=m，DM=n.

AC∥平面MNPQ，MN∥AC，PQ∥AC，MN∥PQ.

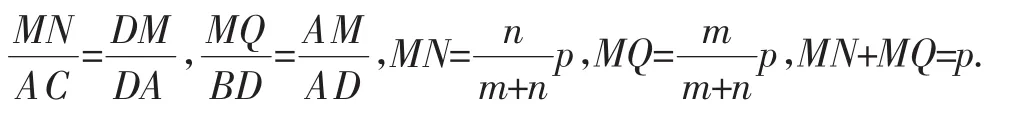
所以四边形MNPQ的周长为2（MN+MQ）=2p.

五、侧面积问题

例5直平行六面体的底面是菱形，过不相邻的两对侧棱的截面面积是p，q.求这个直平行六面体的侧面积.

解：设直平行六面体ABCD-A1B1C1D1的底面菱形的边长为a，高为h.

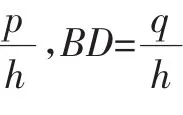
六、体积问题

例6 三棱锥的三个侧面两两垂直，它们的面积分别为S1，S2，S3，求它的体积.

解：如图4所示，在三棱锥P-ABC中，由已知条件可知，三侧棱PA，PB，PC也两两互相垂直，令PA=x，PB=y，PC=z，则：

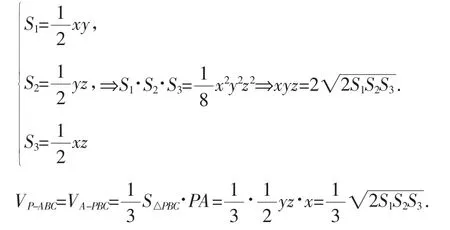
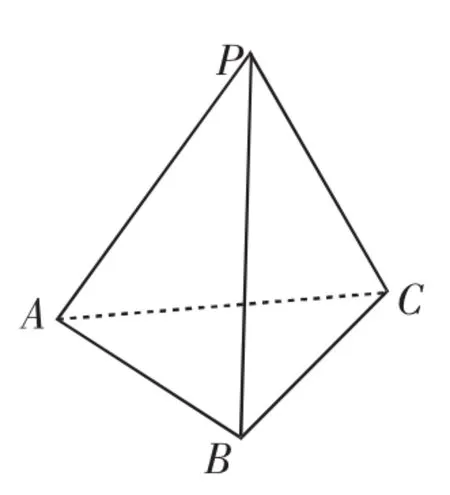
图4

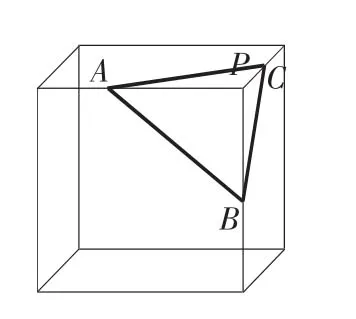
图5

七、截面形状问题

例7将正方体截去一角，求证：截面是一个锐角三角形.

解：如图5，在已知正方体中截去以P为顶点的一角得截面△ABC，令PA=x，PB=y，PC=z.

同时，令BC=a，AC=b，AB=c，PA，PB，PC两两垂直，x2+y2=c2，y2+z2=a2，x2+z2=b2.

∠BAC为锐角.

同理可证，∠ABC，∠ACB也是锐角，因此△ABC为锐角三角形.

八、恒等问题

例8三棱锥P-ABC中，侧棱PA，PB，PC两两互相垂直，三侧面PBC、PAB、PAC与底面分别成角α，β，γ.

求证：cos2α+cos2β+cos2γ=1.

解：如图6，作AD⊥BC于D，作PO⊥AD于O，连接PD，由PA⊥面PBC⇒PD⊥BC⇒∠PDA=α.

图6

设△PBC、△PAB、△PAC、△ABC的面积分别为S1，S2，S3，S，

所以S△OBC=Scos2α.

同理，S△OBA=Scos2β，S△OCA=Scos2γ，S△OBC+S△OBA+S△OCA=S，

Scos2α+Scos2β+Scos2γ=S，cos2α+cos2β+cos2γ=1.

九、定值问题

例9如图7，P为长方体ABCD-A1B1C1D1的对角线AC1上一动点，设PC与面AC成α角，PD与面C1D成β角，求证：tan αtan β为定值.

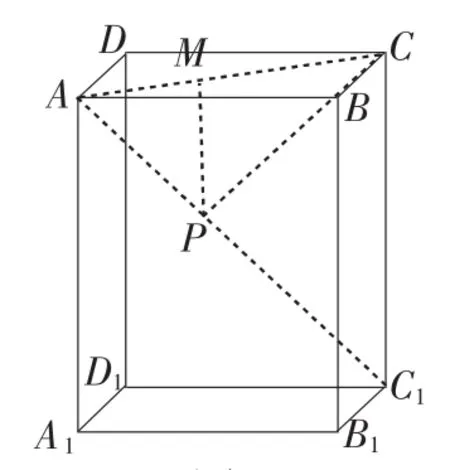
图7

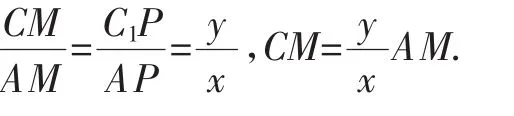
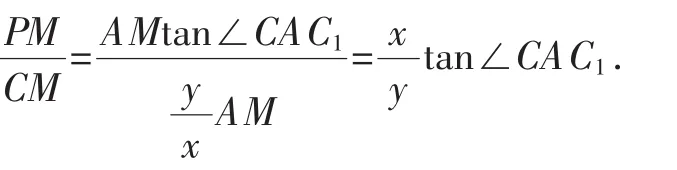
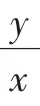
图8

十、最值问题

例10用一块钢锭烧铸一个厚度均匀，且表面积为2平方米的正四棱锥形的有盖容器（如图8），设容器的高为h米，盖子边长为a米.

（1）求a关于h的解析式.

（2）设容器的容积为V立方米，则h为何值时，V最大？

求出V的最大值（不记容器厚度）.

解：（1）设h′是正四棱锥的斜高，由题设可得：

十一、综合问题

例11已知三棱锥各个侧面与底面成60°角，底面三角形的各角成等差数列，且最大边和最小边是方程3x2-21x+13=0的两根，求三棱锥的体积.

解：作三棱锥V-ABC的高VO，则O为△ABC的内心.可设△ABC的三个内角∠A，∠B，∠C，成等差数列，对应边为a，b，c，内切圆的半径为r.

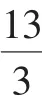
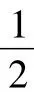
十二、高考问题

例12（2007天津高考第19题）如图9，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点.

（1）证明：CD⊥AE；

（2）证明：PD⊥平面ABE；

（3）求二面角A-PD-C的大小.

解：（1）（2）略.

图9

（3）作AM⊥PD，垂足为M，连结EM，设PA=a，易证：AE⊥PC，AE⊥PD，AE⊥面PDC.

AM在平面PCD内的射影是ME，则EM⊥PD，∠AME是二面角A-PD-C的平面角.

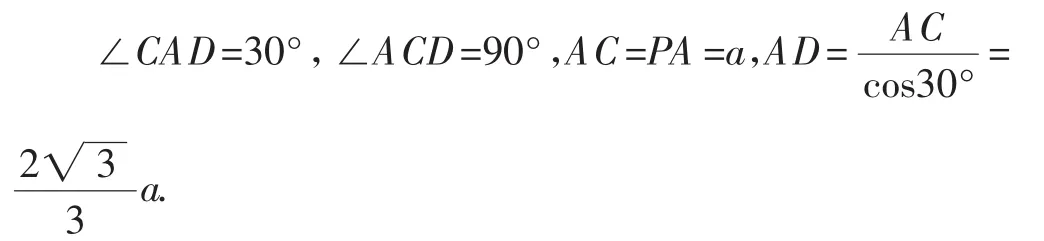
由此可见“设而不求”的思想在立体几何问题中用途很广，对此进行探索和研究，对提高思维的灵活性，简化立体几何中的运算，创造性思维的培养都大有裨益.