无额外自由度广义有限元的近不可压弹-塑性分析

马今伟, 段庆林

(1. 大连理工大学 工业装备结构分析优化与CAE软件全国重点实验室, 辽宁 大连 116024;2. 大连理工大学 大连理工大学白俄罗斯国立大学联合学院, 辽宁 大连 116024)

0 引 言

近或完全不可压分析中的体积自锁一直是有限元分析难题[1],它具有多种触发形式,例如线弹性材料中无限接近0.5的Poisson比、橡胶等超弹性材料中趋于无穷的体积模量以及金属等材料塑性应变的流动方向都会引起有限元分析中的体积自锁．从插值的角度解释:常规有限元的简单形函数难以做到不违背体积近似不变约束的同时,正确反应材料和结构的变形响应．解决体积自锁的思路大体上可以分为两种:第一种是放松约束,最典型的代表是混合格式中的u-p方法[2];以及纯位移格式中的选择减缩积分[3]和平均体应变[4]方法．第二种思路是采用更加丰富的近似函数,如高阶单元中的8节点四边形单元和20节点六面体单元;以及p型方法中的等几何分析、无单元Galerkin法、h-p云团法等,广义有限元就是p型方法的一种．

广义有限元是有限元的自然延伸,它通过引入强化函数极大地丰富了常规有限元的近似空间,并广泛应用于裂纹扩展[5-6]、并行计算[7]等问题的模拟．传统的广义有限元中,强化函数的构造需要引入额外自由度,这不仅扩大了问题的求解规模,额外自由度同标准自由度之间的线性相关性还会导致刚度阵奇异．针对该问题,目前已发展了多种方法,如稳定广义有限元[8]、正交广义有限元[9]等．Tian[10]提出了无额外自由度的强化函数,它的构造仅需标准自由度,从而消除了线性相关性问题．这种方法与常规有限元法具有相同的计算流程,且不增加求解规模,差别仅在于近似函数不同．Xiao等[11]将这种方法推广到了扩展有限元,并应用于裂纹扩展问题的研究．Ma等[12-13]将其推广到了弹塑性固体的大变形分析中．在这些应用中,无额外自由度广义有限元展现出了计算精度高、收敛稳定、网格扭曲健壮等方面的优点．

大量数值分析表明,采用高阶近似函数能有效提高其近不可压分析的能力,如:Elguedj等[14]采用不同阶次的等几何单元进行了线弹性、超弹性以及塑性材料的近不可压分析;Chen等[15]采用再生核粒子法对橡胶梁进行了大变形分析以及塑性杆的颈缩分析等．本文的主要研究内容就是探究无额外自由度广义有限元的近不可压分析能力．

1 无额外自由度广义有限元插值函数

无额外自由度广义有限元对标量函数的插值可以写为

(1)

其中,E为点x所在单元,NI为标准有限元形函数,uI(x)为定义在节点I处的局部近似函数,表示为

(2)

(3)

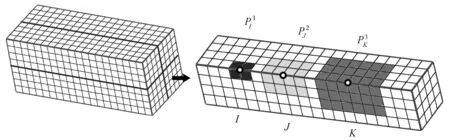
图1 节点patch示意图Fig. 1 Schematic diagram of patches

其中,p(x)为基底向量,它的常数形式以及二阶和三阶形式分别写为

(4)

(5)

(6)

2 非线性广义有限元节点内力线性化

控制方程弱形式的离散化可以写为

(7)

(8)

(9)

3 近不可压线弹性小变形分析

线弹性小变形分析忽略几何效应,且本构模量为常量．式(9)中考虑

(10)

其中,μ和λ为Lamé常数,后者与弹性模量E及Poisson比υ的关系可写为λ=υE/((1+υ)(1-2υ)),与体积模量κ的关系为κ=λ+2μ/3．当υ趋近于0.5时,λ和κ趋近于无穷,这意味着结构几乎只能发生纯剪切变形,而体积不能发生膨胀和压缩．

采用经典的Cook膜问题考察无额外自由度广义有限元在近不可压线弹性分析中的表现．Cook膜算例的描述可参见文献[14]．分别采用常数形式以及式(4)中二次和三次的基底向量来考察插值函数的阶次对缓解体积自锁的效果．为方便阐述,我们将采用这3种基底的方法分别表述为constant-base GFEM、quadratic-base GFEM和cubic-base GFEM．Poisson比设置为υ=0.499 9,计算网格和3种方法计算得到的变形及y方向位移云图如图2所示．

图2 Cook膜算例中GFEM采用3种基向量计算的位移场和变形Fig. 2 Displacement fields and deformations obtained with the GFEM for constant, quadratic and cubic bases in the Cook membrane exmaple

采用不同密度的4种网格考察3种基底的收敛性．这些网格厚度方向始终保持为3个单元,另两个方向的单元数分别为3×3, 6×6, 9×9, 15×15．粗略来说,右上角顶点处的位移的参考解在7.9～8.0之间,收敛性测试结果如图3所示．

图3 Cook膜算例中GFEM采用3种基向量在不同密度网格下收敛性测试结果Fig. 3 Convergence results of the GFEM for constant, quadratic and cubic bases in the Cook membrane example

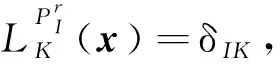
4 近不可压超弹性大变形分析

橡胶是典型的超弹性材料,其本构方程通过联系第二PK应力Sij和Green应变张量Ekl给出:

(11)

(12)

其中,FiI为变形梯度．这里考察超弹性橡胶梁的纯弯曲,算例的描述及Mooney-Rivlin橡胶可参见文献[12]．采用隐式分析流程,将梁的弯矩载荷均分为100步施加,并将体积模量分别设置为κ=104,105,106,107．图4和图5分别展示了FEM和GFEM在第1,10,30,60,100个载荷步中梁的变形过程．

图4 FEM在纯弯曲橡胶梁中的变形Fig. 4 Deformations obtained with the FEM in the pure bending rubber beam example

图5 GFEM在纯弯曲橡胶梁中的变形Fig. 5 Deformations obtained with the GFEM in the pure bending rubber beam example

5 近不可压J2塑性分析

J2塑性的屈服函数可写为

(13)

(14)

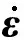
(15)

其中,λ为塑性乘子,n为塑性流动方向．

塑性材料的变形过程中,塑性应变远大于弹性应变,而塑性应变流动只能沿着偏应变方向进行,这意味着塑性变形是纯剪切变形,体积无法发生膨胀或压缩．需要说明的是,塑性变形与加载路径相关,为保证收敛及避免可能出现的伪卸载现象需要采用正割的Newton-Raphson迭代法．此外,屈服面附近发生弹性到塑性的突变,需要采用基于应力更新算法的一致切线模量来提高收敛性．正割的Newton-Raphson迭代方法可参见文献[16]第6章第4节,应力更新算法及一致切线模量的推导可参见文献[17]第3章．

考察圆杆的颈缩问题,算例描述可参见文献[15]．杆的变形集中在局部从而发生颈缩现象,而想要模拟出颈缩现象需要较为精确的内力线性化和较强的近不可压分析能力．图6展示了计算网格以及FEM和GFEM计算的变形及位移场,图7展示了两种方法得到的“顶端位移-颈缩比例”曲线和“顶端位移-支反力”曲线同试验结果的对比,试验数据来源于文献[15]．

(a) 网格 (b) FEM计算的变形及位移场 (c) GFEM计算的变形及位移场 (a) The mesh (b) The FEM in the necking bar example(c) The GFEM in the necking bar example

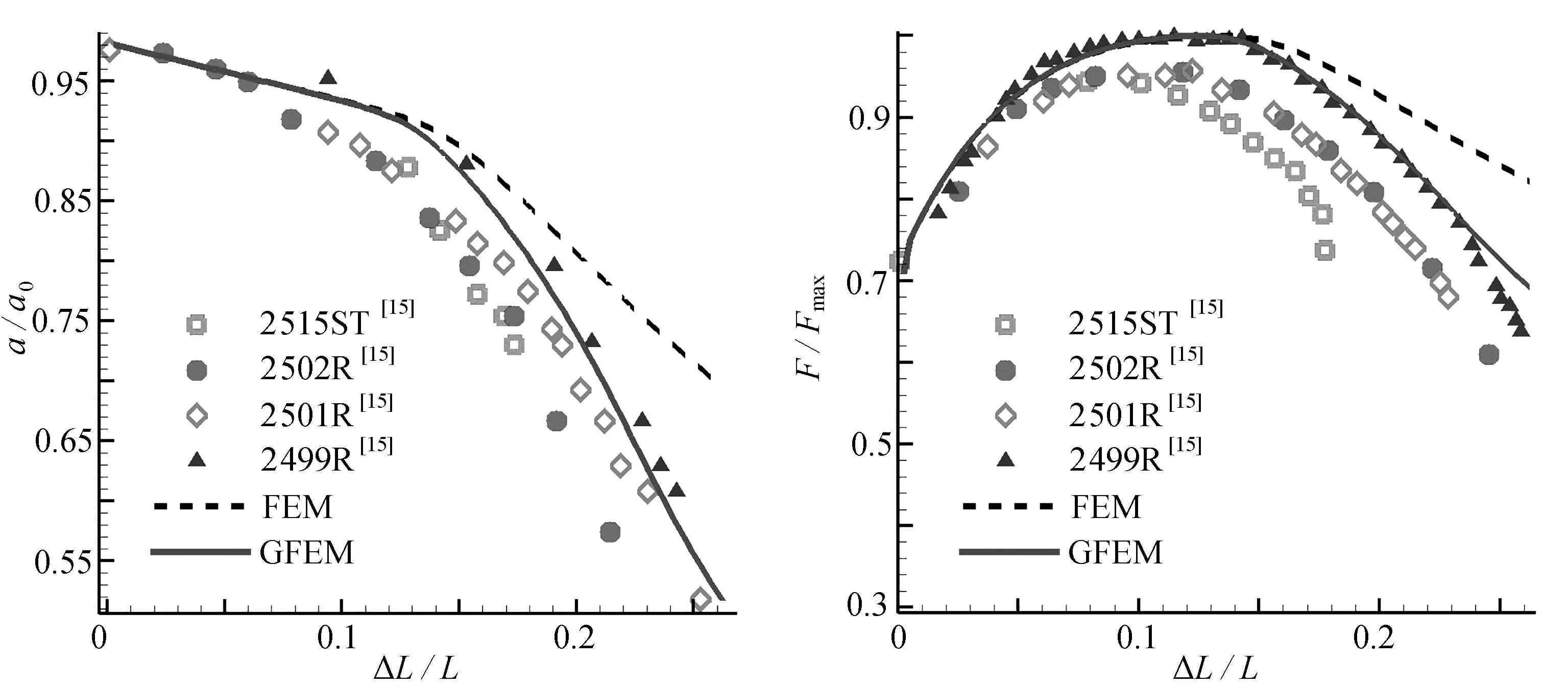
图7 圆杆颈缩算例中FEM和GFEM数值结果与试验结果[15]的对比Fig. 7 Comparison between experimental data[15] and numerical results in the necking circular bar example

6 结 论

本文在弹性、超弹性及塑性不可压分析中,得出了如下结论:

1) 弹性问题的不可压性体现在Poisson比接近0.5时．在Cook膜算例中可以看出,采用常量形式基底向量的广义有限元,也就是常规有限元,存在非常严重的体积自锁问题,体积自锁的缓解效果随着插值阶次的提高而变得更好．

2) 超弹性材料的不可压性体现在超大的体积模量,常规有限元随着体积模量的增大表现出愈发严重的体积自锁,而广义有限元方法能有效缓解这种体积自锁．

3) 塑性材料的不可压性体现在塑性流动只能沿着偏应变方向,导致塑性变形中体积不会膨胀和压缩．在圆杆颈缩算例中,常规有限元无法模拟颈缩现象,而采用二次基底的广义有限元可以．

致谢本文作者衷心感谢大连理工大学中白国际合作基金(ICR2203)对本文的资助．