例析求参数取值范围的方法

曹　昕　　　　　洪家凤

(安徽省涡阳县第二中学,233600)　(安徽省涡阳县第四中学,233600)



例析求参数取值范围的方法

曹昕洪家凤

(安徽省涡阳县第二中学,233600)(安徽省涡阳县第四中学,233600)

在高中数学中,求某个参数的取值范围是很常见的一种题型.由于这类问题涉及的知识点多,用到的数学思想方法也较多,故常受到高考命题专家的青睐,也能很好的体现《考试大纲》中“在知识交汇处命题,以能力立意”的高考宗旨.这类问题思维要求高,解法灵活,学生不易掌握,教师教起来也感觉困难.为了便于读者的教与学,笔者对此类问题加以总结,列出常见类型的求解方法,希望能对读者有所帮助.

一、分类讨论法

分析该题为已知函数的极小值求参数值,只要确定f(x)在(0,e)内的极小值点即可.

解f(x)的定义域为(0,+∞),

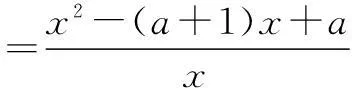
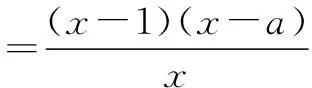
① 当a>1时,令f′(x)>0,得0a，∴f(x)在(0,1)和(a,+∞)内单调递增,在(1,a)内单调递减，此时

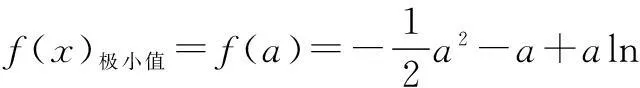
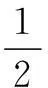
② 当a=1时,f′(x)恒大于等于0,不可能有极小值.

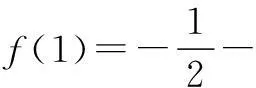
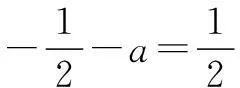
综上，a=-1.

评注函数极值问题与函数的单调性息息相关,若函数f(x)在x=x0的左边导函数值负,右边导函数值正,则x=x0是函数f(x)的极小值点;反之,则x=x0是函数f(x)的极大值点.

二、分离参数法

例2(2013年全国高考题)已知函数f(x)=x2+ax+b,g(x)=ex(cx+d).若曲线y=f(x)和y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.

(1)求a,b,c,d的值；

(2)若x≥-2时,f(x)≤kg(x),求k的取值范围.

分析(2)对x的值分三类讨论将k分离出来,分别求出k的范围再取交集.

解(1)a=4,b=2,c=2,d=2(过程略).

(2)由(1)知f(x)=x2+4x+2,g(x)=2(x+1)ex.

①当x=-1时,易见k∈R.

② 当-2≤x<-1时,

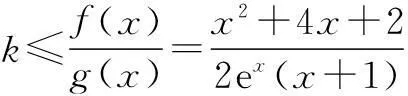
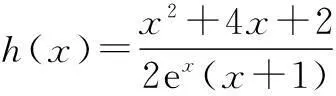
∴y=h(x)在[-2,-1)上递增，

k≤(h(x))min=h(-2)=e2.

③ 当x>-1时,

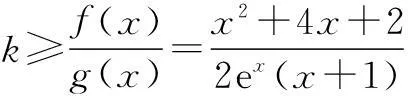
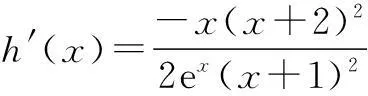
∴当x∈(-1,0)时,h′(x)>0;

当x∈(0,+∞)时,h′(x)<0.

故k≥h(x)max=h(0)=1.

综上，所述k的取值范围为[1,e2].

评注分离参数法，就是将参数与主变元分离于式子的两边,再结合主变元的范围确定含主变元的式子的范围.若参数k≤f(x)恒成立,则k≤f(x)min;

若参数k≥f(x)恒成立,则k≥f(x)max.这种方法可避开繁琐的分类讨论,使得问题的解决简单快捷.

三、构造函数法

例3(2014年江苏高考题)已知函数f(x)=ex+e-x,其中e是自然对数的底数.

(1)证明:f(x)是R上的偶函数;

(2)若关于x的不等式mf(x)≤e-x+m-1在(0,+∞)内恒成立,求实数m的取值范围;

分析第(2)问:

途径1:利用分离参数解决恒成立问题,分离后构造函数,用求导的方法求出最值，这是中学常见的解题策略;

途径2:将不等式变形移项后构造适当的函数,并对函数进行分析,从而解决问题.

解法1已知不等式变形为

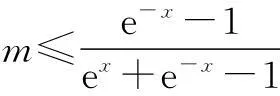
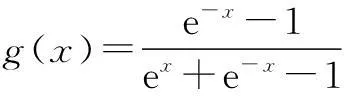
解法2由已知得me2x-(m-1)ex+m-1≤0在x∈(0,+∞)内恒成立.

构造函数

g(x)=me2x-(m-1)ex+m-1,

其中x∈(0,+∞).

令ex=u>1.则

g(u)=mu2-(m-1)u+m-1(u>1).

由g(u)≤0，得

评注分离参数后构造函数是解决恒成立问题的通法,很多时候会避免讨论,给解题带来简便.把不等式变形后构造函数,也是解决问题的常用方法,要合理地把握,合理地变通,在数学教学中要让学生抓住通法进行思考,就能顺利解答.

四、数形结合法

例4已知函数f(x)=x3-3ax+2,求当方程x3-3ax+2=0分别有三个不同的实根及有唯一的实根时a的范围(其中a>0).

分析方程x3-3ax+2=0有三个不同的实根,就是函数f(x)=x3-3ax+2的图象与x轴有三个不同交点.利用导数研究函数f(x)=x3-3ax+2的图象,数形结合可知:只要函数f(x)的极大值大于0,极小值小于0时即可使方程x3-3ax+2=0有三个不同的实根；当极大值与极小值同号时有唯一实根.

解函数的定义域为R,其导函数为

f′(x)=3x2-3a.

x(-∞,-a)-a(-a,a)a(a,+∞)f'(x)+0-0+f(x)递增极大值递减极小值递增

根据列表讨论,可作函数的草图(如图1)

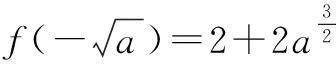
评注一些抽象的数学问题存在着形象的直观模型,在解题时有意识地去挖掘抽象问题的直观形象,变抽象为形象,由数思形,

数形结合,往往可以起到意想不到的效果.在解决这类问题时，如果给定的一个函数,其图象的大致轮廓能清晰地呈现在我们面前，一些数学问题也就能顺利地得到解决.方程根的个数或者说函数零点的个数问题是数形结合思想的一个具体的应用.

五、特殊值巧解法

例5(2013年全国高考题)已知函数

若|f(x)|≥ax,则a的取值范围是()

(A)(-∞,0] (B)(-∞,1]

(C)[-2,1](D)[-2,0]

分析若按分类讨论的方法去解决本题费时费力,一般的学生是很难完成的.考虑到题目是选择题,可用特殊值法排除.观察选项我们不难发现A,D选项没有1,不妨令a取1,则显然有ln(x+1)>x不成立,即a不能取1,这样答案就在A,D中选择.再观察A,D选项有何不同呢?A中有-3,D中没有.令m取-3,显然有|f(x)|=x2-2x≥-3x,x≤0不成立.这样很容易选出正确答案D.

六、 一元二次方程根的分布法

例6若x2-ax+a=0在(-3,4)内有两个不等的实数根,求a的取值范围.

解令f(x)=x2-ax+a.

由题意，知

评注解决二次函数根的分布问题，需关注抛物线的开口方向、对称轴方程、区间端点处函数值、判别式Δ,结合其图象分析以上四个方面便可将问题解决.