本是同根生　相互有联系
——说说数列这一特殊函数

钱佳玲　刘　霞

(江苏省梅村高级中学，214112)



本是同根生相互有联系
——说说数列这一特殊函数

钱佳玲刘霞

(江苏省梅村高级中学，214112)

不管是数列还是函数,都是高考中比较重要的考察部分.苏教版必修1第二章函数的概念:一般地,设A、B是两个非空的数集,如果按照某种对应法则f,对于集合A中的每一个元素x,在集合B中都有唯一的元素y和它对应,那么这样的对应叫做从A到B的一个函数，通常记为y=f(x),x∈A，其中,所有的输入值x组成的集合叫做函数y=f(x)的定义域,所有输出的y值组成的集合称为函数的值域.从这个概念，我们可以看到函数有三要素:定义域、对应关系、值域．根据这个定义，数列也可以看成一类特殊的函数,特殊性在于定义域是正整数,那么数列对应的图象当然应该是一个一个孤立的点．由于这个特殊性,一些数列的问题就可以用函数的知识来解决了．

一、会用函数知识解决数列的问题

既然数列是特殊的函数,用函数的知识来解决数列的一些问题.

例1已知数列{an}的前n项和为Sn,Sn=n2-4n+6,求Sn的最小值．

分析由于数列可以看成特殊的函数,那么Sn就可以看成是关于n的二次函数,由对称轴n=2,可以快速得出这个数列前n项和的最小值为2．

例2等差数列{an}中,已知a1=25,S9=S17,则此数列前多少项和最大?

分析由于公差不为0的等差数列的Sn=An2+Bn,由题可知这个二次函数的对称轴为n=13,所以前13项和最大．

反思上面两个题目利用函数的知识都可以快速的解决,简单方便,但是这里涉及到的对称轴恰好是整数,若不是整数,就需要我们抓住数列的特殊性,避免发生错误．

例3在数列{an}中,a1=1,a2=5,an+2=an+1-an(n∈N*),则a2014=______.

解法1通过递推关系式,可以一一列举出a3=4,a4=-1,a5=-5,a6=-4,a7=1等,由此发现这是一个以6为周期的一个循环过程．所以只需看从1到2 014中有几个这样的周期就可以了．

∴a2014=a4=-1.

解法2题目的条件,其实已告诉我们有f(n+2)=f(n+1)-f(n)这样的抽象函数关系式,且n∈N*.

∵f(n+2)=f(n+1)-f(n)，

①

∴f(n+3)=f(n+2)-f(n+1).

②

①+②，得f(n+3)=-f(n).

以n+3代n,得f(n+6)=f(n).

从上式可以看出此抽象函数以6为周期且每隔两项的值是相反的,还可以得出每个周期的项的和为0,同样可以得到a2014=a4=-1.

评注解法2很巧妙的利用了抽象函数的知识解决了数列的问题,使得此数列的特征更加明显．

二、抓住特殊性,精准做题

在利用函数知识解决数列问题的时候,往往会忽略数列的特殊性而导致错误．这时候一定要认准数列的特殊性,抓住其本质,才能做到精准解题．

例4已知数列{an}的前n项和为Sn,Sn=n2-5n+6,求Sn的最小值．

分析Sn是关于n的二次函数,但是这个二次函数的对称轴为n=2.5,由于数列的特殊性,n只可取正整数,当n=2或3时,Sn都能取到最小值0．

例5已知数列{an}是递增数列,且an=n2+λn,求实数λ的取值范围.

解法1∵{an}是递增数列，

∴an+1>an对n∈N*恒成立，

即(n+1)2+λ(n+1)>n2+λn

对n∈N*恒成立，得

λ>-(2n+1)

对n∈N*恒成立.因此λ大于数列{-(2n+1)}的最大值-3，即λ>-3.

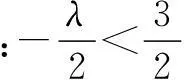
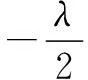
例6设a>0,若

且{an}是递增数列,则实数a的取值范围是______.

错解∵{an}是递增数列

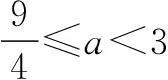
分析上述解法把此数列完全等同于分段函数，没有考虑到数列是个特殊的函数,自变量n∈N*,对应的图象为一个个孤立的点,其实在分段点处不需要考虑绝对的递增性,只需保证a7

正解∵{an}是递增数列

“本是同根生”,抓住函数这一条根,兼顾数列的不同点,在用函数思想解决数列问题的同时,又能关注到数列这一条“藤”,注意数列的特殊性,必定可以对数列有一个更深刻的了解．